Простые виды сопротивления. Растяжение и сжатие

Пример деловых игр для выявления умений и навыков практического применения знаний

1 деловая игра.

Проведение первичного инструктажа на рабочем месте токаря с практическим показом безопасных приемов и методов труда.

2 деловая игра.

Оказание первой помощи пострадавшему при поражении электрическим током.

Вопросы для рефлексивного анализа ситуации к участникам ролевой игры:

• Удовлетворены ли Вы результатами своих действий и почему?

• Поделитесь переживаниями, которые Вы испытывали в ходе

игры. Чем вызваны эти переживания?

• Хотели бы Вы что-то изменить, оказавшись вновь в такой ситуации, и что именно?

• Чем Вам помогал и/или мешал партнер в поисках правильного решения задач своей роли?

• Может ли Вам пригодиться нынешний опыт, если да, то в каких обстоятельствах реальной жизни?

3.1. Внутренние усилия и напряжения при растяжении (сжатии)

Растяжение (сжатие) – простой вид сопротивления, при котором стержень нагружен силами, параллельными продольной оси стержня и приложенными в центр тяжести его сечения.

Рассмотрим стержень упруго растянутый центрально приложенными сосредоточенными силами F.

Прежде чем перейти к исследованию внутренних усилий и напряжений, возникающих в растянутом стержне, рассмотрим некоторые гипотезы, связанные с характером деформирования такого стержня и имеющие в сопротивлении материалов исключительно важное значение.

Принцип Сен-Венана: в сечениях, достаточно удаленных от мест приложения сил, распределение напряжений и деформаций мало зависит от способа приложения нагрузок.

Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи от точек приложения внешних сил (см. рисунок) и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи.

Гипотеза плоских сечений (гипотеза Я. Бернулли): поперечные сечения стержня плоские и перпендикулярные его оси до деформации остаются плоскими и перпендикулярными оси и после деформации (см. рисунок).

Используя метод мысленных сечений, определим внутренние усилия в растянутом стержне:

а) стержень, нагруженный растягивающими

силами F и находящийся в равновесии, рассекаем произвольным сечением;

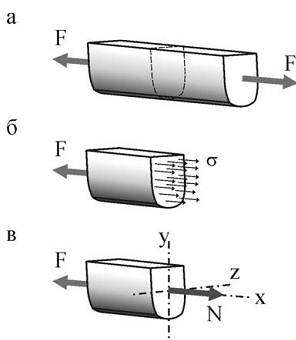
б) отбрасываем одну из частей стержня, а ее действие на другую часть компенсируем внутренними усилиями, интенсивностью σ;

в) осевое внутреннее усилие N, возникающее в сечении стержня, определим, составляя уравнения равновесия для отсеченной части:

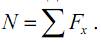
Проецируя внешнюю силу F, действующую на отсеченную часть стержня, на другие оси (y и z), а также составляя уравнения моментов относительно координатных осей, легко убедится, что осевое усилие N является единственным внутренним усилием, возникающим в сечении стержня (остальные тождественно равны нулю).

Таким образом, при растяжении (сжатии) из шести внутренних усилий в сечении стержня возникает только одно – осевое усилие N.

Нормальные напряжения σx, возникающие в сечении стержня, связаны с осевым усилием N следующим образом:

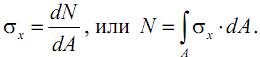
Учитывая, что в соответствии с гипотезой Бернулли напряжения равномерно распределены по поперечному сечению (т. е. σx=const), можно записать:

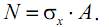
Таким образом, нормальные напряжения при растяжении (сжатии) определяются как

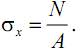
3.2. Перемещения и деформации при растяжении (сжатии)

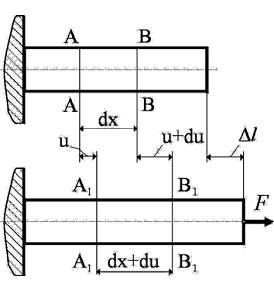
Рассмотрим стержень, находящийся под действием растягивающей нагрузки. Выделим (до деформации) два произвольных сечения стержня А–А и B–B, отстоящие друг от друга на расстоянии dx. От приложенной нагрузки сечение А–А переместиться в положение А1–А1 на расстояние u, а сечение B–B – в положение B1–B1 на расстояние u+du (du – бесконечно малая величина). Следовательно, абсолютное удлинение отрезка dx равно разности его размеров до и после деформации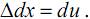

Относительная продольная деформация точек сечения A–A стержня при растяжении

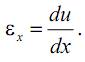
Для линейно-упругого материала относительная деформация при растяжении связана с нормальными напряжениями по закону Гука:

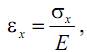
или, учитывая, что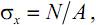

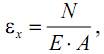
здесь Е – модуль нормальной упругости (модуль Юнга), постоянный коэффициент, который является конста нтой материала (например, для стали Е=2·1011Па, для меди Е=1·1011Па, для титана Е=1,2·1011Па).

Исходя из этих формул, можно записать выражение для перемещений точек растягиваемого стержня в рассматриваемом сечении

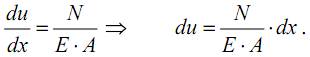
Тогда, полное удлинение стержня при растяжении ∆l, равное перемещению точек правого крайнего сечения, относительно левого крайнего:

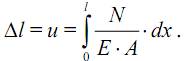
При постоянстве величин N, А, E вдоль оси стержня, абсолютное удлинение можно найти так:

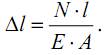
При растяжении стержень деформируется не только в продольном направлении, но и в поперечном.

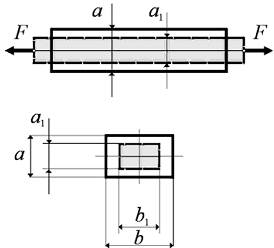
Абсолютная поперечная деформация стержня определяется как разность его поперечных размеров до и после деформации:

Относительная поперечная деформация стержня определяется отношением абсолютной поперечной деформации к соответствующему первоначальному размеру.

Относительная поперечная деформация при растяжении (сжатии) для изотропных материалов во всех направлениях одинакова:

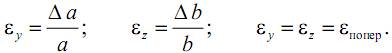
Между поперечной и продольной относительной деформациями при растяжении (сжатии) в пределах применимости закона Гука существует постоянное соотношение, которое называется коэффициентом поперечных деформаций (коэффициентом Пуассона µ).

Коэффициент Пуассона равен абсолютной величине отношения поперечной деформации к продольной

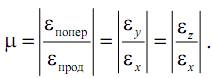
Коэффициент Пуассона – безразмерная величина.

Так как продольная и поперечная деформация для большинства конструкционных материалов имеют противоположные знаки, можем записать

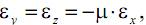
или, учитывая, что, согласно закону Гука,

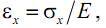
запишем

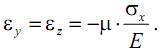
Коэффициент Пуассона µ наряду с модулем Юнга E характеризуют упругие свойства материала. Для изотропных материалов коэффициент Пуассона лежит в пределах от 0 до 0,5 (пробка µ≈0; сталь µ≈0,3; каучук µ≈0,5).

3.3. Расчеты на прочность и жесткость при растяжении (сжатии)

Одна из основных задач сопротивления материалов – обеспечить надежные размеры деталей, подверженных тому или иному силовому, температурному или другому воздействию. Указанные размеры можно определить из расчета на прочность или жесткость. Рассмотрим условия прочности и жесткости для случаев простого растяжения (сжатия). Опасность наступления разрушения характеризуется величинами наибольших нормальных и касательных напряжений, возникающих при нагружении в опасных (т. е. наиболее напряженных) точках сечения. Очевидно, что реальные материалы не могут выдерживать сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми значениями, такими, чтобы деталь испытывала только упругие деформации. Их называют допускаемыми напряжениями. При растяжении и сжатии допускаемые напряжения обозначают [σ+], [σ–] соответственно (принято также обозначение σadm).

Если из расчета известны максимальные и минимальные (по алгебраической величине) напряжения, возникающие в опасном сечении детали, то условия прочности могут быть записаны следующим образом:

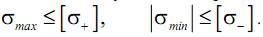
Если материал одинаково сопротивляется растяжению и сжатию, что характерно для пластичных материалов (более строго–для материалов в пластичном состоянии), а значит [σ+]=[σ–]=[σ], то

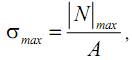
и условие прочности при растяжении (сжатии) запишем в виде:

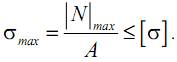
В некоторых случаях для обеспечения нормальной работы машин и сооружений размеры их деталей нужно выбирать так, чтобы обеспечивалось условие жесткости, то есть ограничить предельные деформации (перемещения) элементов конструкции.

Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид:

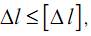
где ∆l – изменение размеров детали; [∆l] – допускаемая величина этого изменения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин ∆l по участкам

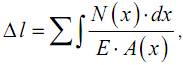
условие жесткости при растяжении (сжатии) запишем следующим образом:

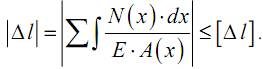
3.4. Допускаемые напряжения. Коэффициент запаса прочности. Виды расчетов

Итак, размеры деталей необходимо подбирать таким образом, чтобы под действием приложенных нагрузок элемент конструкции не разрушался и не получал деформаций, превышающих допустимые. Отметим при этом, что в большинстве машиностроительных деталей не допускается возникновение остаточных деформаций под действием эксплуатационных нагрузок.

Как показывают механические испытания (испытания на растяжение и сжатие), раз рушен и е хрупких материалов начинается, когда напряжения в сечении элемента конструкции превысят величину временного сопротивления (предела прочности) σв. Поэтому для хрупких материалов, деформация которых, как правило, незначительна, за опасное (предельное) напряжение следует принимать именно предел прочности σв:

σ =σ.

Для пластичных материалов за опасное (предельное) напряжение следует принимать предел текучести σт (или условный предел текучести σ0,2, если площадка текучести отсутствует), так как за пределом текучести в пластичных материалах возникают значительные пластические деформации, приводящие при сбросе нагрузки до нуля к появлению остаточных напряжений, следовательно:

σ =σ.

Естественно, что эти опасные напряжения не могут быть использованы в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения гарантированно были меньше опасных, а деформации были упругими. Таким образом, допускаемое напряжение может быть определено по формуле

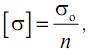
где σо – опасное напряжение; n – коэффициент запаса прочности.

Допускаемые напряжения – это наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы.

Выбор коэффициента запаса прочности зависит от состояния материала

(хрупкое или пластичное), характера приложения нагрузки (статическая, динамическая или повторно-переменная) и некоторых общих факторов, основными из которых являются:

1) различие механических характеристик материала в лабораторных образцах и реальной детали;

2) неточность задания величины внешних нагрузок;

3) неточность расчетных схем и приближенность методов расчета;

4) учет конкретных условий работы рассчитываемой конструкции;

5) долговечность и значимость проектируемого сооружения или машины.

Для конструкционных сталей значение коэффициента запаса прочности принимается n=1,4…1,6; для хрупких материалов n=2,5…3; для древесины n=3,5…6. Тогда величина допускаемых напряжений для среднеуглеродистых сталей [σ]=140…180 МПа; для высоколегированных [σ]=200…400 МПа.

Используя условие прочности, можно решать три типа задач:

1) проектировочный расчет – по известным нагрузкам для известного материала найти надежные с точки зрения прочности размеры поперечного сечения стержня (спроектировать прочную деталь);

2) проверочный расчет – по заданным размерам и материалу детали проверить, может ли она выдержать приложенную нагрузку;

3) расчет по несущей способности (грузоподъемности) – по известным размерам детали, материалу и схеме нагружения определить допустимую величину нагрузки на деталь.

3.5. Понятие о концентрации напряжений

Равномерное распределение напряжений по сечению растянутого стержня сохраняется только в случае, если сечения стержня остаются постоянными по его длине. Резкие изменения площади поперечного сечения вследствие наличия поперечных отверстий, выточек, канавок, надрезов приводят к неравномерному распределению напряжений (вызывают концентрацию напряжений) и называются концентраторами напряжений.

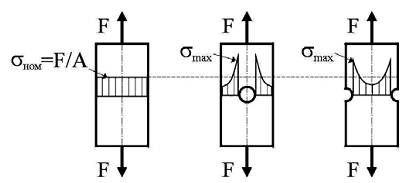
При исследовании явления концентрации напряжений вводят понятия номинального напряжения, наибольшего местного напряжения и коэффициента концентрации напряжений.

Номинальное напряжение – напряжение, вычисленное на основе предположения об отсутствии концентрации напряжений.

При растяжении номинальное напряжение вычисляется как

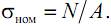
Наибольшее местное напряжение – максимальное напряжение, действующее в месте концентрации напряжений.

Местные напряжения, действующие в области концентратора напряжений, могут быть найдены теоретически – методами теории упругости, либо экспериментально – непосредственным измерением при помощи специальных приборов и методик.

Коэффициент концентрации напряжений – отношение максимального местного напряжения к номинальному напряжению

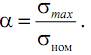
Коэффициент концентрации зависит от вида концентратора, размеров и формы образца, а также свойств материала.

Дата добавления: 2014-01-13