Теорема Пуассона

Схема испытаний Бернулли.

Схема независимых испытаний

План.

В поле заземлителя

1. Схема независимых испытаний

2. Схема испытаний Бернулли.

3.Теорема Пуассона.

4.Локальная теорема Муавра-Лапласа.

5.Интегральная теорема Муавра-Лапласа.

На основании введенного понятия вероятностного пространства рассмотрим одну часто встречающуюся на практике схему.

Пусть в некотором опыте мы можем получить конечное число элементарных исходов 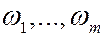, вероятности которых нам известны 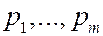. Пусть мы проводим серию из n таких опытов и интересуемся вероятностью наблюдения той или иной последовательности элементарных исходов. Будем считать, что результаты любого опыта не влияют на результаты других опытов. Такие опыты называются независимыми.

Опишем эту схему в терминах теории вероятностей.

Пусть одиночному опыту соответствует вероятностное пространство 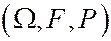, где .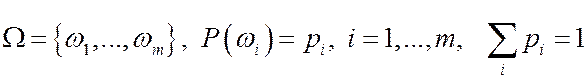

Тогда двукратному повторению этого опыта можно поставить в соответствие вероятностное пространство , то есть , .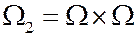
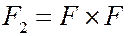В этом случае элементарными исходами для 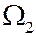будут всевозможные пары

.

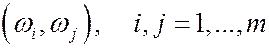Поскольку по условию опыты независимы, то вероятность Р ₂ определим в виде:

.

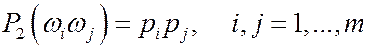Аналогично, обобщив это на n опытов, введем следующее определение

Определение. Пусть 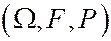- заданное вероятностное пространство, такое что .

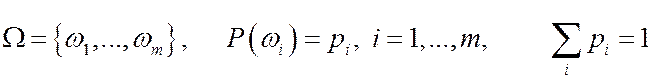Последовательностью n независимых испытаний называется вероятностное пространство

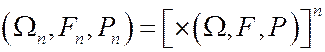, для которого элементарными исходами являются последовательности 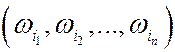, а вероятности элементарных исходов определяются по формуле .

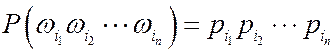Далее будем рассматривать частный случай этой схемы, когда 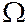состоит из 2-х исходов.

Определение. Последовательностью независимых испытаний называется схемой Бернулли, если 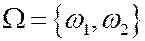, то есть опыт имеет только два исхода.

Исход 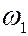принято называть успехом и соответствующую ему вероятность обозначим .

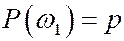Исход 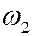принято называть неудачей и соответствующую ему вероятность обозначим .

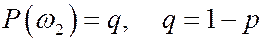В серии из n независимых испытаний Бернулли всего 2ⁿ исходов, причем

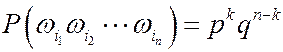, где k – число успехов в серии .

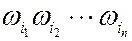Рассмотрим задачу: Какова вероятность в серии из n независимых испытаний Бернулли получить 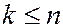успехов, неважно в каких именно опытах.

Интересующее нас событие является объединением таких 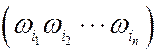, в которых исход 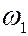встречается k раз. Таких событий 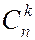штук и, поскольку они несовместны, то вероятность их суммы равна сумме вероятностей и

.

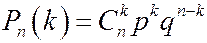Такие вероятности называются биномиальными, поскольку 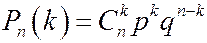есть члены разложения бинома 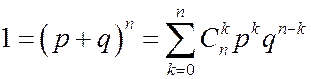. Глядя на эту формулу, еще раз убеждаемся, что сумма всех вероятностей равна 1.

Исследуем поведение 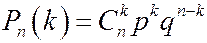при изменении k:

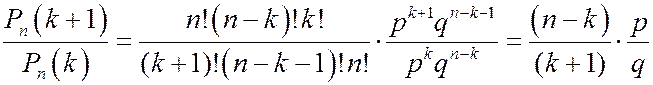
Неравенство 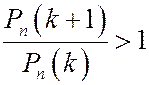эквивалентно неравенствам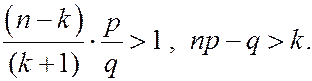

Т.О. 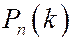сначала возрастает (пока 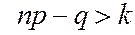), а затем убывает. Значение k, при котором достигается максимум 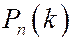называется наиболее вероятным числом успехов. Если np-q – не целое, то k=[np-q]+1, если np-q – целое число, то максимальных вероятностей будет две .

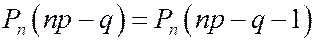Если np-q<0, то 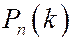убывает с ростом k и наиболее вероятным числом успехов будет 0.

Вернемся к общей схеме независимых испытаний. Аналогом 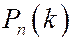в ней будут так называемые мультиномиальные вероятности

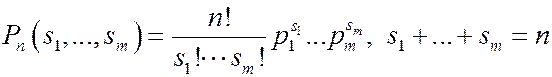- вероятность того, что в n опытах s₁ раз произойдет событие 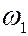, s₂ раз произойдет событие 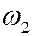, и.т.д.

Формулы биномиальных вероятностей неудобны для вычислений при . Выведем приближенные формулы для 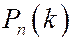для разных случаев.

Теорема Пуассона. Пусть имеется последовательность серий независимых испытаний, такая что при 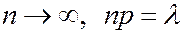(то есть p с ростом n уменьшается, но так, что ).

Тогда, при фиксированном k .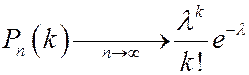

Доказательство.

.

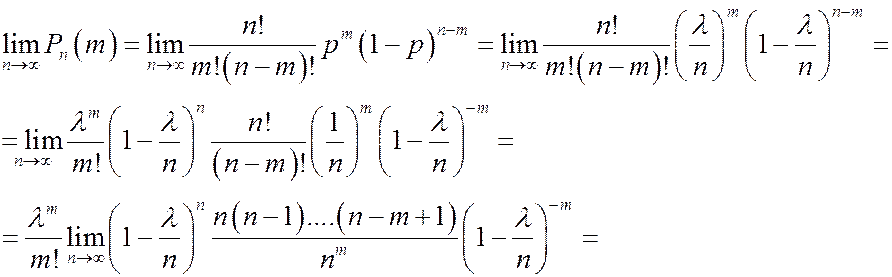
Набор вероятностей 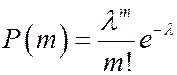называется распределением Пуассона.

Пример 1:

Вероятность зарегистрировать частицу счетчиком равна 10^-4. Какое наименьшее число частиц должно пролететь через счетчик, чтобы с вероятностью не менее 0.8 счетчик зарегистрировал не менее 2-х частиц.

Решение.

Пусть n – искомое число частиц. Будем считать, что производится n опытов с вероятностью успеха р =10^-4. Введем событие А=(счетчик зарегистрировал не менее 2-х частиц).

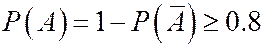. Таким образом .

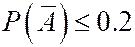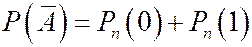. По формуле Пуассона получим, что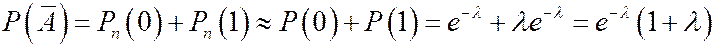

Численным расчетом можно найти, что 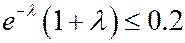при .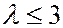

При этом частиц.

Уточненная теорема Пуассона (без док-ва). Пусть А — произвольное множество целых неотрицательных чисел, 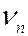— число успехов в испытаниях схемы Бернулли с вероятностью успеха p, 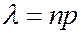. Тогда

.

Для приведённого выше примера

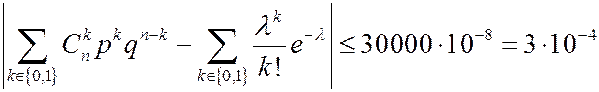
Теперь рассмотрим случай, когда р не стремится к нулю с ростом n.

Дата добавления: 2014-01-13