Наилучшее приближение в гильбертовом пространстве

Выше в пункте 2.11 рассматривалась задача о приближении функции, заданной таблично. Однако задачу о приближении функции можно сформулировать и в более общем виде, а именно в терминах теории приближений в линейных нормированных пространствах.

Пусть дано линейное нормированное пространство 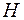, может быть бесконечномерное, и в нем задана конечная система линейно независимых элементов

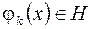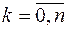, . (2.41)

Требуется приближенно заменить заданный элемент 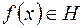линейной комбинацией

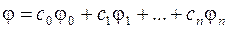(2.42)

Элемент 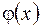, определенный согласно (2.42), называется обобщенным многочленом, построенным по системе элементов (2.41).

Будем рассматривать задачу о наилучшем приближении, состоящую в том, чтобы для заданного 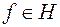среди всех линейных комбинаций вида (2.42) найти такой обобщенный многочлен 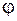, для которого отклонение

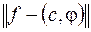(2.43)

было бы минимальным. Элемент 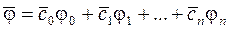, дающий решение этой задачи, называется элементом наилучшего приближения.

Известно, что при весьма общих предположениях элемент наилучшего приближения существует и единствен.

Рассмотрим задачу о наилучшем приближении в том случае, когда 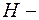вещественное гильбертово пространство со скалярным произведением и нормой 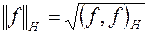. Типичным примером гильбертова пространства является пространство 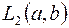вещественных функций 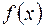, интегрируемых с квадратом на 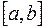, причем

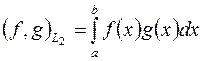, (2.44)

Пусть задана конечная система линейно независимых элементов 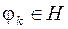, 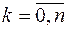. В данном случае задача о наилучшем приближении состоит в том, чтобы для заданного элемента 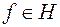найти обобщенный многочлен

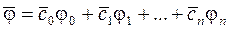, (2.45)

для которого отклонение

(2.46)

является минимальным среди всех обобщенных многочленов вида

.

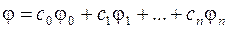Можно доказать, что сформулированная задача имеет единственное решение, которое находится из системы уравнений:

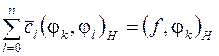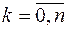, . (2.47)

Таким образом, элемент наилучшего приближения в пространстве имеет вид (2.45), где коэффициенты 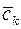, 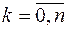отыскиваются из системы (2.47).

Алгоритм построения элемента наилучшего приближения в гильбертовом пространстве состоит в следующем:

1) вычисление элементов 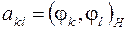, 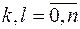матрицы ;

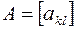2) вычисление правых частей , :

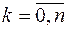3) решение системы (2.47);

4) вычисление суммы .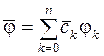

Как правило, каждый из этих этапов алгоритма осуществляется приближенно, с помощью численных методов. Например, в случае пространства 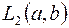необходимо уметь вычислять интегралы

,

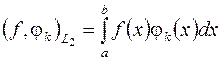что можно сделать, вообще говоря, лишь приближенно.

Оценим теперь отклонение 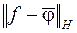, которое получается в результате использования наилучшего приближения в гильбертовом пространстве.

Можно показать, что если 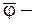элемент наилучшего приближения в 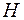, то

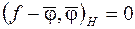, (2.48)

т.е. погрешность 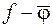ортогональна элементу наилучшего приближения.

Тогда, если 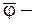элемент наилучшего приближения в 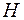, то

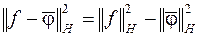. (2.49)

Доказательство следует из тождества

и равенства (2.48).

Наиболее часто среднеквадратичные приближения используются в том случае, когда система 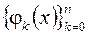ортонормированна, т.е.

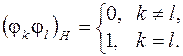
Тогда система (2.47) решается в явном виде:

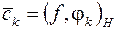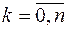, , (2.50)

а погрешность приближения определяется формулой

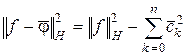. (2.51)

Числа 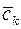, определенные согласно (2.50), называются коэффициентами Фурье элемента 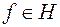по ортонормированной системе 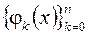, а обобщенный многочлен

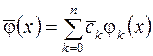
называется многочленом Фурье.

Дата добавления: 2014-01-13