
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И высот облопачивания
|
|
|
|
В основе любых расчетов, связанных с определением площадей лопаточных венцов, лежит использование уравнения неразрывности (1.6), которое допускает два подхода:
а) расчет по торцевым площадям и действительным углам выхода потока;
б) расчет по узким сечениям межлопаточных каналов.
Основные геометрические величины, которые используются далее, показаны на рис.1.2.
При расчете по торцевым площадям уравнение неразрывности с учетом формул (1.29) и (1.30) записывается для соплового и рабочего венцов так:
 ,
,  .
.
Выразив торцевые площади венцов через их геометрические размеры, получим:
 ,
, 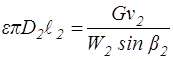 ,
,
отсюда:
 , (2.28)
, (2.28)
 , (2.29)
, (2.29)
Здесь  - степень впуска [1]
- степень впуска [1]  ,
,  - высоты сопловых и рабочих лопаток в сечениях 1-1 и 2-2;
- высоты сопловых и рабочих лопаток в сечениях 1-1 и 2-2;  ,
, 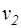 - удельные объемы рабочей среды в точках 1 и 2 схемы процесса течения в I - S - диаграмме (см. рис.2.1);
- удельные объемы рабочей среды в точках 1 и 2 схемы процесса течения в I - S - диаграмме (см. рис.2.1); 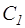 ,
,  ,
,  ,
,  скорости и углы выхода потока при действительном истечении из соплового и рабочего венцов, с учетом их осреднения, о котором сказано выше.
скорости и углы выхода потока при действительном истечении из соплового и рабочего венцов, с учетом их осреднения, о котором сказано выше.
В практике расчет чаще ведется по площадям узких сечений (называемых горлом) межлопаточных каналов. Если О1 – «горло» каналов сопловой решетки, О2 – «горло» каналов рабочей решетки, то
 ,
, 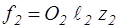 (2.30)
(2.30)
Здесь  и
и  - число сопловых и рабочих лопаток в решетках соответственно;
- число сопловых и рабочих лопаток в решетках соответственно;  ,
, - суммарные площади «горл» этих решеток.
- суммарные площади «горл» этих решеток.
Используем понятия:  - эффективный угол выхода потока из сопел;
- эффективный угол выхода потока из сопел;  - эффективный угол выхода потока из рабочих лопаток (в относительном движении). Запишем:
- эффективный угол выхода потока из рабочих лопаток (в относительном движении). Запишем:
 ,
,  (2.31)
(2.31)
где  и
и  - шаг сопловых и шаг рабочих лопаток соответственно.
- шаг сопловых и шаг рабочих лопаток соответственно.
Умножив и поделив правые части выражений (2.30) на  и
и  , получим с учетом равенства (2.31):
, получим с учетом равенства (2.31):
 ,
,  (2.32)
(2.32)
Вспоминая, что  ,
,  , определим площади
, определим площади  и
и  в следующем виде:
в следующем виде:
 ,
,  (2.33)
(2.33)
Напомним, что для осевой ступени 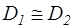 .
.
При расчете по узким сечениям в уравнение неразрывности вводят вместо действительных скоростей изоэнтропические и вместо действительных удельных объемов - удельные объемы в конце изоэнтропических процессов расширения. Для увязки действительного расхода с его теоретическим значением используют понятие «коэффициент расхода», о котором говорилось выше. Тогда уравнения неразрывности для сопловой и рабочей решеток можно записать в виде:
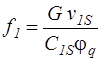 ,
,  . (2.34)
. (2.34)
Из формул (2.34) с учетом выражений (2.33) получаем:
 , (2.35)
, (2.35)
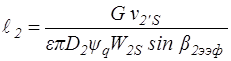 , (2.36)
, (2.36)
где  и
и 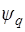 - коэффициенты расхода сопловой и рабочей решеток соответственно.
- коэффициенты расхода сопловой и рабочей решеток соответственно.
Напомним, что в реальных решетках профилей площадь сечения потока от узкого до выходного сечения несколько меняется, поэтому действительный угол на 1-2° отличается от эффективного.
Коэффициент расхода учитывает наличие пограничного слоя на периметре узкого сечения решетки, неравномерность поля скоростей в этом сечении и отличие величины средней скорости в нем от скорости, сосчитанной по перепаду на решетку.
Формулы (2.28), (2.29), (2.35), (2.36) относятся к докритическому истечению из лопаточных венцов.
При сверхкритических перепадах давления расчет высот облопачивания можно производить по формулам (2.28), (2.29), исходя из торцевых площадей венцов, и по формулам (2.35) и (2.36) - по площадям узких сечений межлопаточных каналов.
Применительно к рассматриваемому случаю формулы (2.28), (2.29) дают следующее:
 , (2.37)
, (2.37)
 . (2.38)
. (2.38)
Здесь углы 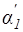 и
и  - углу выхода потока из сопел и рабочих лопаток, с учетом расширения потока в косом срезе. С1 и W2 действительные скорости, найденные с учетом потерь.
- углу выхода потока из сопел и рабочих лопаток, с учетом расширения потока в косом срезе. С1 и W2 действительные скорости, найденные с учетом потерь.
Величины углов 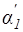 и
и  можно рассчитать по формуле Бэра:
можно рассчитать по формуле Бэра:
 , (2.39)
, (2.39)
 , (2.40)
, (2.40)
где  и
и  - углы выхода потока в критическом сечении;
- углы выхода потока в критическом сечении;  - теоретическая скорость, соответствующая изоэнтропическому перепаду энтальпий, определяемому перепадом давлений от
- теоретическая скорость, соответствующая изоэнтропическому перепаду энтальпий, определяемому перепадом давлений от 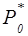 (точка О* на диаграмме I - S) до
(точка О* на диаграмме I - S) до  (см. рис.2.1);
(см. рис.2.1);  - то же, но при перепаде давлений от
- то же, но при перепаде давлений от  (точка 1* на диаграмме I - S, см. рис.2.1) до
(точка 1* на диаграмме I - S, см. рис.2.1) до  ;
;  ,
,  - теоретические скорости, соответствующие изоэнтропическому течению.
- теоретические скорости, соответствующие изоэнтропическому течению.
Удельные объемы берутся на изоэнтропах  ;
; 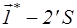 .
.
Для использования при расчете формул (2.37)-(2.40) необходимо иметь достаточно точные зависимости коэффициентов потерь в соплах и рабочих лопатках от  и
и 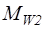 , а также значения
, а также значения  и
и  при критическом истечении. Эти данные не всегда есть на начальной стадии проектирования. Поэтому чаще для расчетов высот
при критическом истечении. Эти данные не всегда есть на начальной стадии проектирования. Поэтому чаще для расчетов высот  и
и  при сверхкритических перепадах давлений используют выражения (2.35) и (2.36), которые применительно к нашему случаю принимают следующий вид:
при сверхкритических перепадах давлений используют выражения (2.35) и (2.36), которые применительно к нашему случаю принимают следующий вид:
 , (2.41)
, (2.41)
 . (2.42)
. (2.42)
Расчет расширяющихся сопел может вестись по торцевым площадям и по площадям узких сечений. Если давление за соплом окажется более низким, чем в его выходном сечении (т.е. ниже расчетного давления, соответствующего заданному отношению площадей), следует учесть расширение в косом срезе расширяющихся сопел [3].
Формулы (2.1)-(2.42) представляют собой алгоритм расчета, позволяющего на заданном режиме работы турбинной ступени последовательно провести расчет соплового и рабочего венцов, построить входной и выходной треугольники скоростей и определить высоты и проходные сечения каналов сопловых аппаратов и венцов рабочих колес.
При тепловом расчете ступени с заданными геометрическими размерами, противодавлением и частотой вращения, но с нерасчетным расходом остаются в силе все формулы, использованные в п.п. 2.1-2.3. Однако в этом случае расчет удобно проводить не по ходу пара, а в обратном направлении, выполняя его, как говорят, «с конца» - от сечения 2-2 за рабочими лопатками к сечению 0-0 перед сопловыми. В результате расчета определяются давления в контрольных сечениях 1-1 и 0-0 ступени, степень реактивности, мощность и кпд.
3. ЛОПАТОЧНЫЙ КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
3.1. Вводные замечания и определения
Лопаточным коэффициентом полезного действия (кпд) называют отношение полезной работы на лопаточном венце полностью уплотненной ступени к располагаемой работе, величина которой определяется состоянием рабочего тела перед ступенью и давлением за ступенью.
Обозначим:
 - лопаточный кпд;
- лопаточный кпд;
 - полезная работа (полезно использованный перепад энтальпий);
- полезная работа (полезно использованный перепад энтальпий);
 - располагаемая работа (располагаемый перепад энтальпий).
- располагаемая работа (располагаемый перепад энтальпий).
Тогда по определению:
 . (3.1)
. (3.1)
Полезно использованный в ступени перепад энтальпий [см. формулу (2.27)]
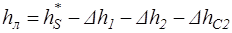
или с учетом формулы (2.2)
 , (3.2)
, (3.2)
где  - располагаемый перепад энтальпий в ступени, определенный по статическим параметрам перед ней и статическому давлению за ней;
- располагаемый перепад энтальпий в ступени, определенный по статическим параметрам перед ней и статическому давлению за ней;  - перепад энтальпий, соответствующий кинетической энергии потока на входе в ступень;
- перепад энтальпий, соответствующий кинетической энергии потока на входе в ступень; 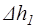 - необратимые потери механической энергии в сопловых лопатках («потери в соплах»);
- необратимые потери механической энергии в сопловых лопатках («потери в соплах»);  - то же в рабочих лопатках;
- то же в рабочих лопатках;  - перепад энтальпий, соответствующий кинетической энергии потока на выходе из ступени, или, как чаще говорят, потери с выходной скоростью.
- перепад энтальпий, соответствующий кинетической энергии потока на выходе из ступени, или, как чаще говорят, потери с выходной скоростью.
Выражение (3.2) является уравнением баланса энергии для турбинной ступени. С другой стороны, в соответствии с турбинным уравнением Эйлера для 1 кг рабочего тела полезная работа  определяется формулой (1.8). Следует отметить, что уравнения (3.2) и (1.8) - лишь различные формы записи одной и той же физической величины и могут быть преобразованы одно в другое путем алгебраических выкладок.
определяется формулой (1.8). Следует отметить, что уравнения (3.2) и (1.8) - лишь различные формы записи одной и той же физической величины и могут быть преобразованы одно в другое путем алгебраических выкладок.
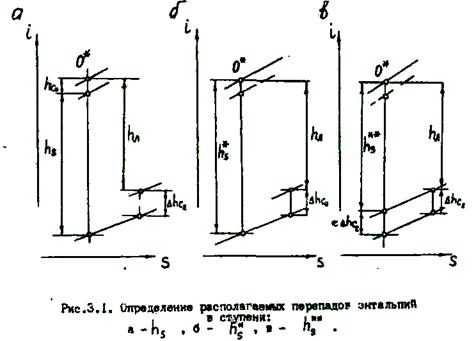
Решение вопроса о выборе величины располагаемого перепада в ступени не однозначно. За располагаемый перепад принимают в разных случаях: величину  , названную выше (рис.3.1,а), величину
, названную выше (рис.3.1,а), величину  (рис.3.1,б), величину
(рис.3.1,б), величину  (рис.3.1,в).
(рис.3.1,в).
В общем случае, при работе турбинной ступени в группе, в ней используется кинетическая энергия потока, поступающего из предыдущей ступени.
С этой точки зрения выбор располагаемых перепадов, показанных на рис.3.1, соответствует предельным теоретически возможным случаям.
Поэтому выражение для располагаемого перепада иногда записывается в таком виде:
 , (3.3)
, (3.3)
где  - коэффициент использования в данной ступени кинетической энергии потока, выходящего из предыдущей ступени;
- коэффициент использования в данной ступени кинетической энергии потока, выходящего из предыдущей ступени;  - коэффициент использования в последующей ступени кинетической энергии потока, выходящего из данной ступени.
- коэффициент использования в последующей ступени кинетической энергии потока, выходящего из данной ступени.
Практически кинетическая энергия потока на входе в ступень используется в различной степени. Для простоты целесообразно ограничиться приведенными предельными трактовками 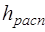 .
.
Располагаемые перепады и другие величины, определенные на базе формулы (3.3) для рассмотренных выше предельных случаев, показаны в табл.3.1.
Принятым различным трактовкам располагаемого перепада ступени соответствуют и отвечающие им трактовки кпд  ,
, 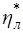 и
и  . Формулы, определяющие в этих случаях величину упомянутых кпд, теоретической скорости и связь последней с выбранным располагаемым перепадом, принимают следующий вид:
. Формулы, определяющие в этих случаях величину упомянутых кпд, теоретической скорости и связь последней с выбранным располагаемым перепадом, принимают следующий вид:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
При конкретных записях расчетных выражений мы будем использовать энергетическую и кинематическую формы их представления.
Рассмотрим энергетическую форму представления кпд. Для этого преобразуем формулу (3.2):
 (3.4)
(3.4)
Располагаемые перепады и лопаточные КПД ступени Таблица 3.1
| № рис. | Параметры | Коэффициенты | Располагаемый перепад 
| Изоэнтропическая скорость 
| Лопаточный КПД | ||
| Во входном сечении 0-0 | В выходном сечении 2-2 | 
| 
| ||||
| 3.1,а | В точке 0 статич-ие Р0, i0 | В точке 2S статич-ое давл-ие Р2 | 
| 
|  по статическим параметрам перед и за ступенью по статическим параметрам перед и за ступенью
| ||
| 3.1,б | В точке 0* заторм-ые Р*0, i*0 | В точке 2S статич-ое давл-ие Р2 | 
| 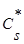
| 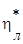 по начальным параметрам тормож-ия и конечному стат-ому давлению по начальным параметрам тормож-ия и конечному стат-ому давлению
| ||
| 3.1,в | В точке 0* заторм-ые Р*0, i*0 | В точке 2’* дав-ие тор-ия Р*2 | 
| 
| 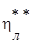 по начальным и конечным парамет-ам торможения по начальным и конечным парамет-ам торможения
|
Введем относительные величины потерь, отнесенные к располагаемым перепадам в ступени.
Например:
 ,
,  ,
,  .
.
При использовании этих величин выражение (3.4) примет вид:
 .
.
(3.5)
Используя общее определение лопаточного кпд (3.1) и выражения (3.5), легко получить формулы, представляющие различные трактовки этого кпд в энергетической форме:
 (3.6)
(3.6)
Исходя из приведенного ранее выражения (1.8), мы можем представить три рассмотренные трактовки лопаточного кпд также в кинематической форме в соответствии с трактовкой понятия располагаемого перепада:
 (3.7)
(3.7)
Напомним, что выражения (3.6) и (3.7) отличаются лишь формой представления. В каждой из записанных групп формул трактовка кпд отвечает той, которая показана в последнем столбце табл.3.1.
Установим области рационального применения и взаимосвязь различных трактовок понятия кпд.
Все трактовки понятия «лопаточный кпд», данные выше, одинаково правомочны, однако для объективного суждения об экономичности ступени каждую из этих трактовок рационально применять в зависимости от конкретных условий: трактовку 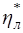 - для ступеней, выходная скорость которых не используется (точнее - кинетическая энергия, соответствующая выходной скорости);
- для ступеней, выходная скорость которых не используется (точнее - кинетическая энергия, соответствующая выходной скорости);  - для ступеней, у которых эта выходная скорость используется в проточной части за ними;
- для ступеней, у которых эта выходная скорость используется в проточной части за ними;  - для ступеней, выходная скорость, в которых равна или близка к входной скорости. В этом случае кпд
- для ступеней, выходная скорость, в которых равна или близка к входной скорости. В этом случае кпд  близок по величине к
близок по величине к  , но применять его при тепловых расчетах групп ступеней удобнее.
, но применять его при тепловых расчетах групп ступеней удобнее.
Установим связь между  ,
, 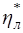 и
и  . Напомним, что
. Напомним, что
 ,
,  ,
,
 ,
,
 ,
,
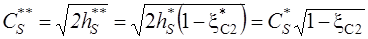 .
.
Поэтому:
 ,
,
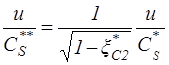 . (3.8)
. (3.8)
Кроме того,
 , (3.9)
, (3.9)
 . (3.10)
. (3.10)
Одним из факторов, существенно влияющих на кпд турбинной ступени, является степень реактивности. Прежде чем говорить об этом влиянии, остановимся на зависимости степени реактивности от геометрических и режимных параметров ступени.
Запишем уравнение энергии (1.11) для контрольных сечений 0-0 и 1-1 соплового венца адиабатической ступени при изоэнтропическом течении:
 .
.
Обозначим разность энтальпий (рис.3.2):
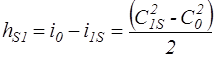 .
.

Эта разность является приращением кинетической энергии пара при его расширении в сопловом венце. Ей соответствует конкретное падение статического давления от Р0 перед венцом до Р1 за венцом. Аналогично, запись уравнения энергии для контрольных сечений 1 и 2 рабочего венца в относительном движении дает:
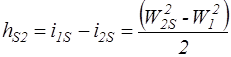 .
.
Величина  называется реактивным перепадом на рабочем венце по статическим давлениям перед и за ним и характеризует увеличение кинетической энергии в рабочих лопатках.
называется реактивным перепадом на рабочем венце по статическим давлениям перед и за ним и характеризует увеличение кинетической энергии в рабочих лопатках.
Для соплового венца вместо перепада  чаще используют величину
чаще используют величину  .
.
Относительная величина реактивного перепада, как было сказано ранее, называется термодинамической степенью реактивности. Так как  , а
, а  , то:
, то:
 . (3.11)
. (3.11)
Одним из основных геометрических параметров ступени, определяющих величину  , является отношение площадей узких сечений каналов рабочих и направляющих лопаток
, является отношение площадей узких сечений каналов рабочих и направляющих лопаток 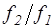 . При одномерном течении в уплотненной ступени массовые расходы пара через рабочий и сопловой венцы равны:
. При одномерном течении в уплотненной ступени массовые расходы пара через рабочий и сопловой венцы равны:  или, используя уравнение неразрывности:
или, используя уравнение неразрывности:
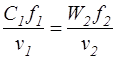 ,
,
 . (3.12)
. (3.12)
Отношение  зависит от
зависит от  и от отношения давлений
и от отношения давлений 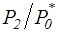 . Если характеризовать последнее приведенной скоростью
. Если характеризовать последнее приведенной скоростью  , то как показывают расчеты, при
, то как показывают расчеты, при  в зависимости от величины
в зависимости от величины  > 0 отношение
> 0 отношение  < 1,1…1,15. Следовательно, в указанном диапазоне изменения
< 1,1…1,15. Следовательно, в указанном диапазоне изменения 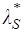 , который соответствует большинству ступеней цилиндров высокого давления (ЦВД) и цилиндров среднего давления (ЦСД) современных конденсационных турбин, влияние сжимаемости не является решающим. Поэтому, пренебрегая для простоты этим влиянием, положим
, который соответствует большинству ступеней цилиндров высокого давления (ЦВД) и цилиндров среднего давления (ЦСД) современных конденсационных турбин, влияние сжимаемости не является решающим. Поэтому, пренебрегая для простоты этим влиянием, положим 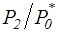 >0,97;
>0,97;  и перепишем уравнение (3.12) так:
и перепишем уравнение (3.12) так:
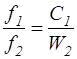 . (3.13)
. (3.13)
Учитывая формулы (3.12) и (2.18)
 ,
,
 .
.
Из треугольников скоростей (рис.1.4)
 .
.
После преобразований получим из (3.13):
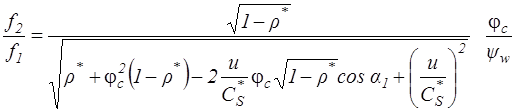 . (3.14)
. (3.14)
На режимах работы турбинной ступени, мало отличающихся от расчетного, отношение 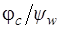 меняется сравнительно мало. При учете этого обстоятельства оказывается, что выражение (3.14) при
меняется сравнительно мало. При учете этого обстоятельства оказывается, что выражение (3.14) при 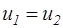 связывает отношение площадей
связывает отношение площадей 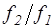 и угол
и угол  определяющие геометрию ступени «в главном», с режимными параметрами:
определяющие геометрию ступени «в главном», с режимными параметрами:  и
и  . При умеренных значениях
. При умеренных значениях  влияние этого угла в выражении (3.14) не существенно.
влияние этого угла в выражении (3.14) не существенно.

Для большей наглядности рассмотрим зависимость 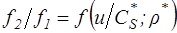 , построив соответствующие графики, приняв
, построив соответствующие графики, приняв  =16°,
=16°,  и не учитывая сжимаемость. Эти графики показаны на рис.3.3. Анализируя их, можно сделать следующие выводы:
и не учитывая сжимаемость. Эти графики показаны на рис.3.3. Анализируя их, можно сделать следующие выводы:
- при фиксированном значении  и заданной конструкции соплового аппарата (
и заданной конструкции соплового аппарата ( =const) с уменьшением отношения
=const) с уменьшением отношения 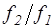 степень реактивности в ступени возрастает. Влияние
степень реактивности в ступени возрастает. Влияние 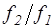 на ее величину является решающим;
на ее величину является решающим;
- при фиксированном значении степени реактивности  отношение
отношение 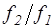 с увеличением отношения
с увеличением отношения  становится больше. Интенсивность роста отношения площадей максимальна при
становится больше. Интенсивность роста отношения площадей максимальна при  =0 и уменьшается по мере возрастания
=0 и уменьшается по мере возрастания  . Большим степеням реактивности соответствуют малые величины отношения
. Большим степеням реактивности соответствуют малые величины отношения 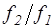 и наоборот.
и наоборот.
Следует отметить, что при таком подходе к рассмотрению вопроса каждому отношению 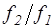 соответствует своя ступень, а при фиксированном значении угла
соответствует своя ступень, а при фиксированном значении угла  - свои профили рабочих лопаток. У конкретной ступени, работающей при переменных
- свои профили рабочих лопаток. У конкретной ступени, работающей при переменных  , отношение
, отношение 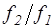 не меняется. Зависимость степени реактивности от
не меняется. Зависимость степени реактивности от  для этого случая будет рассмотрена в последующих разделах курса.
для этого случая будет рассмотрена в последующих разделах курса.
Все сказанное выше о степени реактивности, включая и рассмотрение формулы (3.14), относилось к случаю, когда сжимаемость не оказывала влияния на работу ступени ( 0,97;
0,97;  ).
).
В общем случае с учетом сжимаемости и формулы (3.12)
 ,
,
где  - отношение площадей, найденное без учета сжимаемости.
- отношение площадей, найденное без учета сжимаемости.
В результате рассмотрения вопроса о степени реактивности мы приходим к выводу, что при проектировании ступеней отношение 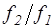 есть функция от
есть функция от  ,
,  ,
, 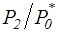 ,
,  . При работе ступени
. При работе ступени  .
.
В дозвуковых ступенях при  определяющей является связь
определяющей является связь 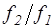 ;
;  ;
;  .
.
В случае малых относительных высот лопаток (при больших отношениях  , о влиянии которых на работу ступени в курсе будет сказано особо), обычно выдерживается соотношение:
, о влиянии которых на работу ступени в курсе будет сказано особо), обычно выдерживается соотношение:  1,1…1,15 и лишь при больших относительных высотах
1,1…1,15 и лишь при больших относительных высотах  1.
1.
В соответствии с уравнением неразрывности
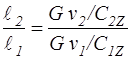 (3.15)
(3.15)
или при 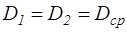 :
:
 . (3.16)
. (3.16)
Учитывая формулы (1.29) м (1.30), из выражений (3.15) и (3.16) имеем:
 , то есть
, то есть 
Обозначим  . Эта величина обычно лежит в пределах 0,9 <
. Эта величина обычно лежит в пределах 0,9 < < 1,5.
< 1,5.
Нижний предел относится к ступеням, срабатывающим малые перепады давлений при дозвуковых скоростях, верхний предел - к сверхзвуковым ступеням с большими перепадами давлений. Величина  меняющаяся в указанных, сравнительно узких пределах, характеризует степень расширения рабочей среды в рабочих лопатках, скорректированную на отношение высот лопаток
меняющаяся в указанных, сравнительно узких пределах, характеризует степень расширения рабочей среды в рабочих лопатках, скорректированную на отношение высот лопаток  . Значения
. Значения  ,
,  ,
,  ,
,  ,
,  и
и  полностью определяют треугольники скоростей и позволяют наглядно провести анализ влияния отдельных факторов на кпд ступени. Перейдем к этому анализу.
полностью определяют треугольники скоростей и позволяют наглядно провести анализ влияния отдельных факторов на кпд ступени. Перейдем к этому анализу.
3.2. ЛОПАТОЧНЫЙ КПД ЧИСТО ОСЕВОЙ АКТИВНОЙ
ТУРБИННОЙ СТУПЕНИ ( )
)
Формула Банки
В общем случае произвольной осевой турбинной ступени изоэнтропический перепад, соответствующий теоретической скорости выхода потока из рабочих лопаток в относительном движении, записывается так:
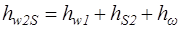 .
.
Здесь  - кинетическая энергия потока на входе в рабочие лопатки в относительном движении;
- кинетическая энергия потока на входе в рабочие лопатки в относительном движении;  - реактивный перепад, срабатываемый на рабочем венце;
- реактивный перепад, срабатываемый на рабочем венце; 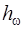 - энергия, преобразуемая в механическую работу посредством кариолисовых сил,
- энергия, преобразуемая в механическую работу посредством кариолисовых сил,  . Согласно принятым допущениям,
. Согласно принятым допущениям,  ;
;  , поэтому
, поэтому  . Учитывая, что по условию
. Учитывая, что по условию  ,
,  =0.
=0.
Таким образом,  =
= и
и  . В соответствии с формулой (2.20)
. В соответствии с формулой (2.20) 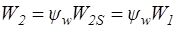 .
.
Легко видеть, кроме того, что в данном случае теоретическая скорость выхода потока из сопел равна теоретической скорости, определенной по располагаемому перепаду на ступень:

при 
 .
.
Поэтому, в соответствии с формулой (2.7):
 .
.
Определим для принятых условий лопаточный кпд, применяя его выражение в кинематической форме (3.7).
Из рассмотрения треугольников скоростей (рис.3.4) имеем:
 ,
,  ,
,
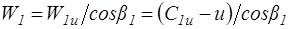 ,
,  ,
,
 .
.
Здесь, как и ранее, за положительное направление проекций скоростей на ось  принято направление по вращению рабочего венца:
принято направление по вращению рабочего венца:
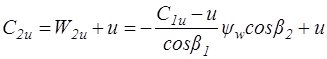 .
.

Найдем разность  :
:

Тогда 
Находя работу на лопатках по уравнению Эйлера [см. формулу (1.8)] и за располагаемый перепад в ступени  , можно записать выражение для кпд на лопатках ступени так:
, можно записать выражение для кпд на лопатках ступени так:

и, наконец, в окончательной форме:
 . (3.17)
. (3.17)
Последнее выражение (3.17) и есть формула Банки.
Прежде чем рассматривать полученный результат, оценим соотношение величин углов  и
и  , входящих в него.
, входящих в него.
Для общего случая одномерного течения в рабочем венце уравнение неразрывности, записанное через торцевую площадь  в сечении 1-1 и
в сечении 1-1 и  в сечении 2-2 имеет вид:
в сечении 2-2 имеет вид:
 .
.
Раскрываем значения площадей и осевых составляющих относительных скоростей:
 .
.
Учитывая, что высоты рабочих и сопловых лопаток отличаются на величину перекрыши 
 , запишем:
, запишем:
 .
.
При записи этого уравнения на величины  и
и  ограничения не накладывались. Для чисто активной ступени при
ограничения не накладывались. Для чисто активной ступени при  =0,
=0, 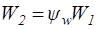 перепишем предыдущее выражение:
перепишем предыдущее выражение:
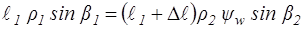 ,
,
откуда:
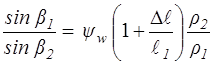 .
.
В рассматриваемом случае  , а произведение
, а произведение  мало отличается от единицы. Поэтому отношение
мало отличается от единицы. Поэтому отношение  , также близко к единице и не зависит от отношения
, также близко к единице и не зависит от отношения  . Однако это отношение влияет на угол
. Однако это отношение влияет на угол  , в связи, с чем с изменением
, в связи, с чем с изменением  и угла
и угла  одновременно должен меняться и угол
одновременно должен меняться и угол  , так чтобы отношение
, так чтобы отношение  .
.
Отсюда вытекает следующее: в чисто активной ступени углы  и
и  мало различаются.
мало различаются.
При фиксированном сопловом аппарате  =idem,
=idem,  =idem каждому отношению
=idem каждому отношению  соответствует свое сочетание углов
соответствует свое сочетание углов  и
и  . Последнее условие означает необходимость при каждом значении
. Последнее условие означает необходимость при каждом значении  использовать разные рабочие лопатки, т.е. разные ступени, что невозможно. Этот же вывод следует из приведенного выше рис.3.3.
использовать разные рабочие лопатки, т.е. разные ступени, что невозможно. Этот же вывод следует из приведенного выше рис.3.3.
С другой стороны, следует помнить, что в конкретной турбинной ступени величина  определяется геометрическими соотношениями рабочей решетки, близка к
определяется геометрическими соотношениями рабочей решетки, близка к  и при непостоянстве
и при непостоянстве  на разных режимах работы меняться не может. Поэтому формула Банки не пригодна для анализа работы конкретной ступени на переменных режимах.
на разных режимах работы меняться не может. Поэтому формула Банки не пригодна для анализа работы конкретной ступени на переменных режимах.
Анализ формулы Банки
Зависимость 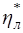 от отношения
от отношения  и других факторов
и других факторов
Формула Банки определяет лопаточный кпд чисто активной ступени как функцию:
- отношения  , однозначно связанного с числом Струхаля Sh [3];
, однозначно связанного с числом Струхаля Sh [3];
- углов  ,
,  ,
,  определяемых геометрическими соотношениями профилей и лопаточных венцов;
определяемых геометрическими соотношениями профилей и лопаточных венцов;
- скоростных коэффициентов  и
и  , в свою очередь зависящих от этих соотношений и параметров
, в свою очередь зависящих от этих соотношений и параметров 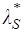 и
и  [3].
[3].
Таким образом, как и следовало ожидать, рассматриваемый кпд зависит от основных критериев работы ступени: отношения  (Sh) и, в неявном виде, от
(Sh) и, в неявном виде, от 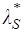 и
и  .
.
Считая, что ступень работает в зоне автомодельности по 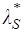 и
и  рассмотрим влияние тех переменных, которые непосредственно, в явном виде, входят в выражение (3.17). В этом случае определяющим является влияние на кпд отношения
рассмотрим влияние тех переменных, которые непосредственно, в явном виде, входят в выражение (3.17). В этом случае определяющим является влияние на кпд отношения  .
.
Оценивая роль этого критерия, полагаем угол  =const (сопловой аппарат при разных
=const (сопловой аппарат при разных  неизменен) и, следовательно, в условиях автомодельности
неизменен) и, следовательно, в условиях автомодельности  =cost.
=cost.
Изменение отношения  и коэффициента
и коэффициента  при изменении
при изменении  является слабым и, как показали расчеты на ЭВМ, при изучении зависимости кпд от
является слабым и, как показали расчеты на ЭВМ, при изучении зависимости кпд от  можно полагать
можно полагать  и
и  постоянными. Напомним еще раз, что каждому, отношению
постоянными. Напомним еще раз, что каждому, отношению  соответствуют свои рабочие лопатки.
соответствуют свои рабочие лопатки.
При этих условиях лопаточный кпд 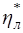 является квадратичной функцией отношения
является квадратичной функцией отношения  . Легко видеть, что
. Легко видеть, что 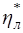 = 0 при
= 0 при  =0 и при
=0 и при 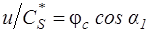 , так что функция
, так что функция 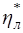 =
=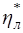 (
( ) должна иметь максимум в промежутке указанных значений
) должна иметь максимум в промежутке указанных значений  .
.
Величину ( )ОПТ (соответствующую максимальному значению кпд (
)ОПТ (соответствующую максимальному значению кпд (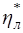 )МАХ) можно найти, взяв производную от выражения (3.17) по
)МАХ) можно найти, взяв производную от выражения (3.17) по  (при сделанных выше допущениях) и приравняв ее нулю:
(при сделанных выше допущениях) и приравняв ее нулю:
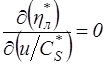 .
.
Далее получим:
 (3.18)
(3.18)
Для одиночной активной ступени, выходная скорость которой не используется, при обычно применяемых значениях  и
и 
 .
.
Зависимость 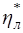 =
=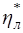 (
( ) представлена на рис.3.5 в виде параболы. Максимальное значение кпд (
) представлена на рис.3.5 в виде параболы. Максимальное значение кпд (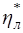 )мах находим после подстановки правой части уравнения (3.18) в уравнение (3.17) вместо отношения
)мах находим после подстановки правой части уравнения (3.18) в уравнение (3.17) вместо отношения  , оно будет следующим:
, оно будет следующим:
 . (3.19)
. (3.19)
Выясним причины параболического характера зависимости 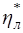 =
=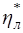 (
( ), представленной на рис.3.5. Для этого, прежде всего, построим треугольники скоростей, характерные для трех случаев:
), представленной на рис.3.5. Для этого, прежде всего, построим треугольники скоростей, характерные для трех случаев:
 ,
,  ,
, 

Это построение выполнено при  =const. Для большей наглядности принято:
=const. Для большей наглядности принято:
- отношение  изменяется за счет окружной скорости u при неизменной скорости
изменяется за счет окружной скорости u при неизменной скорости 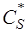 = idem (при этом (
= idem (при этом (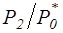 )=idem и располагаемый изоэнтропический перепад энтальпий на ступень не меняется;
)=idem и располагаемый изоэнтропический перепад энтальпий на ступень не меняется;
-  = 0 при всех отношениях
= 0 при всех отношениях  . Следовательно,
. Следовательно,  и сжимаемость не влияет на течение;
и сжимаемость не влияет на течение;
- 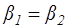 при любом отношении
при любом отношении  , хотя и не постоянны при его изменении;
, хотя и не постоянны при его изменении;
-  и
и  не зависят от
не зависят от  .
.

Треугольники скоростей, построенные, исходя из этих допущений, показаны на рис.3.6. С их помощью рассмотрим одновременное изменение с  отдельных составляющих потерь энергии, пользуясь энергетической формой представления кпд ступени. В соответствии с формулами (3.6)
отдельных составляющих потерь энергии, пользуясь энергетической формой представления кпд ступени. В соответствии с формулами (3.6)
 .
.
Величину  можно раскрыть так:
можно раскрыть так:

(учитывая, что при  = 0,
= 0, 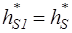 ).
).
Величина  оказывается не зависящей от отношения
оказывается не зависящей от отношения  . Аналогично раскрывается величина
. Аналогично раскрывается величина  :
:
 .
.
Как было показано выше,
 .
.
При  = 0,
= 0,  и
и  . Из рис.3.6 видно, что
. Из рис.3.6 видно, что  становится меньше при увеличении отношения
становится меньше при увеличении отношения  вплоть до
вплоть до  =
=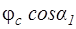 . Соответственно, монотонно уменьшается и
. Соответственно, монотонно уменьшается и  , так что и эта составляющая потерь не может вызвать параболический характер зависимости. [Заметим, что в пределе при
, так что и эта составляющая потерь не может вызвать параболический характер зависимости. [Заметим, что в пределе при  =
=
 , поскольку при этом
, поскольку при этом  и
и  .]
.]
Относительная потеря энергии с выходной скоростью
 .
.
 может быть представлена функцией от
может быть представлена функцией от  , однако она оказывается неявной.
, однако она оказывается неявной.
Из рассмотрения треугольников скоростей, представленных на рис.3.6, следует, что выходная скорость  при неизменной
при неизменной 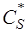 с ростом
с ростом  сперва убывает, затем возрастает. Также меняется отношение
сперва убывает, затем возрастает. Также меняется отношение  . Таким образом, параболический характер зависимости
. Таким образом, параболический характер зависимости 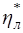 =
=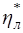 (
( ) в основном определяется изменением относительной потери энергии с выходной скоростью, так как при прочих равных условиях
) в основном определяется изменением относительной потери энергии с выходной скоростью, так как при прочих равных условиях  возрастает при отклонении отношения
возрастает при отклонении отношения  от оптимального значения. Этот результат, а также соотношение величин относительных потерь в ступени показаны на рис.3.7. Если значения
от оптимального значения. Этот результат, а также соотношение величин относительных потерь в ступени показаны на рис.3.7. Если значения  близки к оптимальным, то потери с выходной скоростью имеют тот же порядок величины, что и сумма потерь в лопаточных венцах. При неоптимальных
близки к оптимальным, то потери с выходной скоростью имеют тот же порядок величины, что и сумма потерь в лопаточных венцах. При неоптимальных  потери с выходной скоростью существенно превышают потери в соплах и рабочих лопатках.
потери с выходной скоростью существенно превышают потери в соплах и рабочих лопатках.

Интересно отметить, что при  =(
=( )опт выход потока из ступени - неосевой. Легко показать, что в этом случае:
)опт выход потока из ступени - неосевой. Легко показать, что в этом случае:
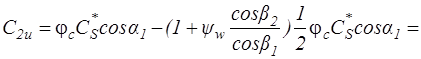
 .
.
Поскольку  <2, выражение, заключенное в квадратные скобки в последней формуле, положительно, вследствие чего
<2, выражение, заключенное в квадратные скобки в последней формуле, положительно, вследствие чего  >0. Это говорит о том, что при
>0. Это говорит о том, что при  =(
=( )опт угол
)опт угол  >90°.
>90°.
Важно отметить, что значение  , соответствующее осевому выходу потока из ступени, а значит и минимуму относительных потерь энергии с выходной скоростыо
, соответствующее осевому выходу потока из ступени, а значит и минимуму относительных потерь энергии с выходной скоростыо  , меньше, чем значение (
, меньше, чем значение ( )опт.
)опт.
Действительно, проведя соответствующие выкладки, получим:
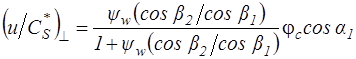 .
.
Величина  < 1, следовательно:
< 1, следовательно:
 .
.
Сопоставляя величину ( )^ с выражением (3.18), приходим к выводу:
)^ с выражением (3.18), приходим к выводу:
( )^<(
)^<( )опт.
)опт.
Заметим, что это соотношение сохраняется и при учете зависимости  от
от  , или при
, или при  ¹0.
¹0.
Рассмотрим теперь зависимость кпд ступени от угла выхода потока из сопел  . Этот угол явно влияет [см. формулу (3.17)] через
. Этот угол явно влияет [см. формулу (3.17)] через 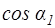 и неявно - через скоростные коэффициенты
и неявно - через скоростные коэффициенты  и
и  . Если бы профильные и концевые потери, связанные с эффектом вязкости, не зависели от углов
. Если бы профильные и концевые потери, связанные с эффектом вязкости, не зависели от углов  ,
,  и
и  , то было бы рационально предельно снижать
, то было бы рационально предельно снижать  для повышения величины
для повышения величины 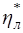 .
.
В действительности, как показано в [4], при неизменной высоте облопачивания уменьшение угла  приводит к увеличению профильных потерь в соплах, а также к росту угла поворота потока в сопловых и рабочих лопатках, и в итоге - к снижению коэффициентов
приводит к увеличению профильных потерь в соплах, а также к росту угла поворота потока в сопловых и рабочих лопатках, и в итоге - к снижению коэффициентов  и
и  . Поэтому существуют оптимальные значения
. Поэтому существуют оптимальные значения  =
= . Расчеты и опыты показывают, что для активных ступеней со сравнительно короткими лопатками
. Расчеты и опыты показывают, что для активных ступеней со сравнительно короткими лопатками  = 10-12°.
= 10-12°.
Расчет по формуле (3.19) показывает, что для чисто активной ступени снижение  на 1% вызывает снижение кпд на ~ 2%, тогда как снижение
на 1% вызывает снижение кпд на ~ 2%, тогда как снижение  на 1% снижает кпд ступени лишь на ~ 0,5%, т.е. на величину, в четыре раза меньшую. Однако следует учитывать, что при значительных степенях реактивности (
на 1% снижает кпд ступени лишь на ~ 0,5%, т.е. на величину, в четыре раза меньшую. Однако следует учитывать, что при значительных степенях реактивности ( > 0) это не так.
> 0) это не так.
Напомним, что объектом приведенного анализа явилась теоретическая модель ступени, у которой изменение проходных площадей рабочих венцов от режима к режиму обеспечивало нулевую степень реактивности. Независимо от величины отношения  , форма лопаток могла быть оптимальной при любом его значении, а угол
, форма лопаток могла быть оптимальной при любом его значении, а угол  - безударным. Такие особенности теоретической модели позволяют, с одной стороны, раздельно оценить влияние каждого из рассмотренных факторов и, с другой стороны, при любом значении
- безударным. Такие особенности теоретической модели позволяют, с одной стороны, раздельно оценить влияние каждого из рассмотренных факторов и, с другой стороны, при любом значении  оперировать минимальными величинами потерь в сопловых и рабочих лопатках и, следовательно, предельными для данного режима значениями лопаточного кпд. И то и другое весьма важно для понимания работы реальной ступени с неизменной геометрией проточной части. Поэтому дальнейший анализ также будем вести применительно к ее теоретической модели.
оперировать минимальными величинами потерь в сопловых и рабочих лопатках и, следовательно, предельными для данного режима значениями лопаточного кпд. И то и другое весьма важно для понимания работы реальной ступени с неизменной геометрией проточной части. Поэтому дальнейший анализ также будем вести применительно к ее теоретической модели.
Основываясь на зависимостях, полученных для коэффициента 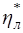 ступени, кинетическая энергия потока на выходе, из которой не используется, перейдем к рассмотрению коэффициента
ступени, кинетическая энергия потока на выходе, из которой не используется, перейдем к рассмотрению коэффициента  ступени, выходная скорость которой используется.
ступени, выходная скорость которой используется.
Зависимость  от
от  и других факторов
и других факторов
Коэффициенты полезного действия  и
и 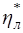 связаны выражением (3.10). Графики
связаны выражением (3.10). Графики  =
= (
( ) и
) и 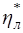 =
=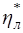 (
(