Векторное произведение

Векторное произведение двух векторов а и b обозначается

a x b

и равно вектору v, который обладает следующими свойствами. Если а = сb для некоторого скаляра с, то v = 0. В противном слу­чае длина вектора v равна

| v | = | a || b | sin g

где g — угол между векторами а и b, а направление вектора v перпендикулярно обоим векторам а и b и таково, что а, b, v, именно в таком порядке, образуют правостороннюю тройку. По­следнее означает, что если вектор а поворачивается на угол g < 180° в направлении к вектору b, то вектор v имеет направле­ние перемещения винта с правой резьбой, поворачиваемого в том же направлении. Из этого определения можно вывести следую­щие свойства векторного произведения:

(kа) х b = k(а х b) для любого вещественного числа k

а x (b + с) = а х b + а х с

a x b = - b х а

В общем случае а х (b х с) ¹ (а х b) х с. Используя правую ортогональную систему координат, как и в пункте 1, с единичными векторами i, j, k, будем иметь

i x i = j x j = k x k = 0

i х j = k, j х k = i, k x i = j

j x i = - k, k x j = -i, i x k = - j

Используя эти значения векторных произведений в расши­ренной записи векторного произведения

а х b = (а₁i + а₂j + а₃k)* (b₁i + b₂j + b₃k)

получим

а х b = (а₂b₃ - а₃b₂)i + (а₃b₁ - а₁b₃)j + (а₁b₂ - а₂b₁)k

что может быть записано в виде

| a₂ a₃ | | a₃ a₁ | | a₁ a₂ |

a x b = çb₂ b₃ú i + çb₃ b₁ú j + çb₁ b₂ú k

или в форме, более удобной для запоминания:

| i j k |

a x b = | a₁ a₂ a₃ |

| b₁ b₂ b₃ |

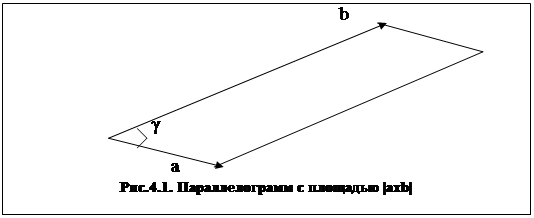
Это скорее мнемоническая запись, чем реальный детерминант, поскольку элементами первой строки являются векторы, а не числа. Если через векторы а и b обозначены соседние стороны параллелограмма, как на рис. 4.1, то площадь этого параллелограмма равна длине вектора а х b. Это непосредственно следует из

| a x b | = | a || b | sin g

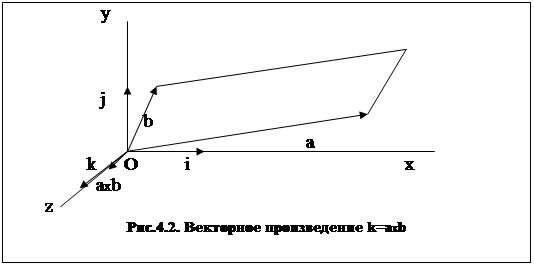
На рис. 4.2 векторы а и b лежат в плоскости, проходящей через оси х и у. Предположим, что ось z выходит из листа бумаги к читателю и соответствует правой координатной системе. Тогда для трехмерного пространства

а = [a₁ a₂ 0], b = [b₁ b₂ 0]

| i j k | | a₁ a₂ |

a x b = | a₁ a₂ 0 | = çb₁ b₂ú k

| b₁ b₂ 0 |

Таким образом, вектор a x b будет иметь то же направление, что и вектор k, но только в том случае, если детерминант

D = | a₁ a₂ |

çb₁ b₂ú

имеет положительный знак. Это налагает условие, что вектор а, поворачиваемый по направлению к вектору b на угол меньше 180°, вращается в положительном направлении (против часовой стрелки) тогда, и только тогда, когда D > 0. Этот способ будем ниже использовать для определения, обходятся ли вершины тре­угольника А, В, С в направлении против часовой стрелки при их перечислении именно в этом порядке. На рис. 4.3 имеем

u = [u₁ u₂] = АВ, v = [v₁ v₂] = АC

| x_A y_A 1 | | x_A y_A 1 |

D = | x_B y_B 1 | = | x_B - x_A y_B - y_A 0 | =

| x_C y_C 1 | | x_C - x_A y_C - y_A 0 |

= | x_B – x_A y_B – y_A | = | u₁ u₂ |

| x_C – x_A y_C – y_A | | v₁ v₂ |

Вершины А, В, С, именно в этом порядке, обходятся в направлении против часовой стрелки, если, и только если, вектор и поворачивается в сторону направления вектора v на угол g < 180° против часовой стрелки. Это означает, что направление обхода точек А, В, С может быть установлено на основе анализа детерминанта

| x_A y_A 1 |

D = | x_B y_B 1 |

| x_C y_C 1 |

следующим образом:

D > 0 - точки А, В, С обходятся против часовой стрелки;

D < 0 - точки А, В, С обходятся по часовой стрелке;

D = 0 - точки А, В, С лежат на одной прямой.

Дата добавления: 2014-01-14