Квадратурные формулы с постоянным весом

Пусть дана квадратурная формула

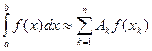(2.1)

Определение. Квадратурная формула

(2.2)

называется подобной формуле (2.1), если

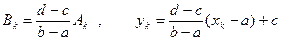(2.3)

Рассмотрим некоторые свойства формул с постоянным весом ().

1. Если АСТ формулы (2.1) 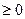, то . ().
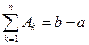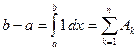2. Если формула (2.2) подобна формуле (2.1), то и формула (2.1) подобна (2.2). Действительно, .
3. Пусть — АСТ формулы (2.1), — АСТ формулы (2.2). Тогда 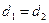. Рассмотрим многочлен степени . Для него формула (2.1) точна: 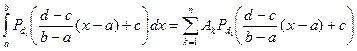. Сделаем замену переменных 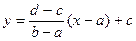. Тогда 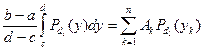. Отсюда . Для многочлена степени имеем 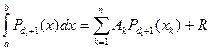. Сделаем замену : , . .
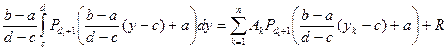4. Из предыдущего свойства следует, что если (2.1) интерполяционная, то и (2.2) интерполяционная.
5. Если формула (2.1) интерполяционная (ИКФ)и ее узлы расположены симметрично относительно середины промежутка (при всех k 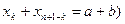, то 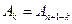. Возьмем промежуток [-1,1]. На нем 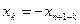. Рассмотрим . Имеем 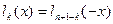. По определению ИКФ (была произведена замена – x на x). В случае произвольного промежутка [ a, b ] достаточно перейти к подобной формуле.

6. Если формула (2.1) интерполяционная и ее узлы расположены симметрично относительно середины промежутка, то ее АСТ есть нечетное число. Рассмотрим 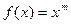на промежутке [-1,1].

Получим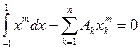если m нечетно. Если же m | четно, то m +1 нечетно и остаток будет равен 0. Значит, первый раз остаток, неравный 0, появится только при четном т.

1. Если ФМК (2.1) имеет представление остатка в форме Лагранжа , где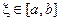, то и (2.2) имеет представление остатка в форме Лагранжа 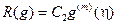, гдеи . Действительно, Положим 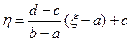. Отсюда .

Далее будем рассматривать некоторые конкретные формулы. При выводе остаточных членов будет полезно использовать следующую лемму:

Лемма. Пусть — интегрируемая функция, причем 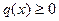, и имеет место точное неравенство на промежутке ненулевой меры, а функция непрерывна на [a,b]. И пусть — произвольное отображение промежутка [a,b] в себя, и существует интеграл . Тогда найдется такая точка , что .

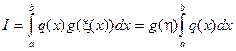Доказательство. Из непрерывности функции 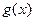следует, что 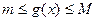для любого . Из неотрицательности 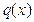следует, что . Отсюда . Проинтегрируем это неравенство:

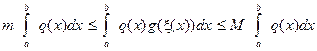. Следовательно,

. Значит, по теореме о среднемнайдется такое , что . Отсюда и вытекает утверждение Леммы.

Теперь перейдем к рассмотрению некоторых конкретных формул.

Дата добавления: 2014-01-14