Формулы типа Гаусса (формулы наивысшей алгебраической степени точности с весовой функцией, отличной от 1)

Формулы типа Котеса.

Квадратурная формула имеет вид:

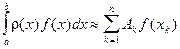
где узлы 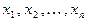определяются по правилу: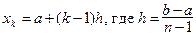, а коэффициенты определяются по обычному правилу для интерполяционной формулы, а именно .

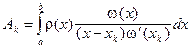По определению, узлами квадратурной формулы типа Гаусса являются корни многочлена, ортогонального с весом 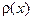ко всем многочленам, степень которых меньше n. Значит, нужно построить такой многочлен. Рассмотрим алгоритм построения такого многочлена, который называется процесс Шмидта.

Будем искать многочлен степени n с неопределенными коэффициентами

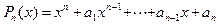(8.1)

Нужно найти n неизвестных коэффициентов. Мы будем искать их, используя условия ортогональности многочлена (8.1) к многочленам 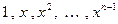. Запишем эти условия:

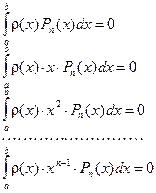(8.2)

Мы получили n соотношений, которые образуют линейную алгебраическую систему относительно n неизвестных коэффициентов А_к. Решив эту систему, получим многочлен P_n (x). Корни этого многочлена и будут узлами квадратурной формулы типа Гаусса с весом .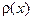

Пример. Построить формулу типа Гаусса с одним узлом с весом 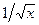на промежутке [0,1]. Многочлен 1-й степени имеет вид: 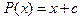. Найдем неизвестный коэффициент c из условия ортогональности P (x) многочлену 0-й степени т.е. 1: . Отсюда c= -1/3. Значит, А=2. Таким образом, получаем

.

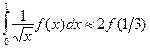Рассмотрим некоторые конкретные весовые функции.

Весовая функция Якоби. (функция 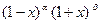, где ).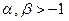

Квадратурная формула:

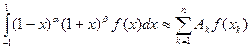. Узлы этой формулы — корни многочлена Якоби степени п, ортогонального с весом 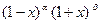на промежутке [ -1, 1 ] ко всем многочленам степени меньше п. Запишем форму Родрига

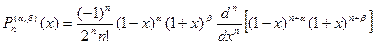. (8.3)

Для 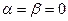это многочлен Лежандра. Получаем формулу Гаусса.

Для получаем многочлен Чебышева. Квадратурная формула с такой весовой функцией называется формулой Мелера.

Дата добавления: 2014-01-14