Представление множеств

End.

Begin

NAME[FREE]¬Х;

NEXT[FREE]¬NEXT[POS];

NEXT[POS]¬FREE;

Нетрудно видеть, что время выполнения процедуры INS не зависит от размера списка.

Пример 3.1. Пусть необходимо вставить в список (3.1) новый элемент NEL (New ELement) после элемента EL2 и получить список

EL1, EL2, NEL, EL3, EL4. (3.2)

Если пятая ячейка (FREE=5) в каждом массиве на рис. 3.2 пуста, можно вставить X=NEL после EL2 (POS=3), вызвав процедуру INS c фактическими параметрами NEL, 5, 3. В результате выполнения трёх операторов в процедуре INS получим NAME[5]=NEL, NEXT[5]=4 и NEXT[3]=5; тем самым создадутся массивы, показанные на рис. 3.3.

Index	NAME	NEXT
	__
	EL1
	EL4
POS®3	EL2
	EL3
	NEL
FREE®6	__	__
Рис. 3.3. Представление списка со вставленным элементом NEL

Ещё две основные операции над списками - конкатенация (сцепление) двух списков, в результате которой образуется единственный список, и обратная к ней операция расцепления списка после заданного элемента, результатом которого будут два списка.

Конкатенацию можно выполнить за ограниченное (постоянной величиной) число шагов, включив в представление списка ещё один указатель. Этот указатель даёт индекс последней компоненты списка и тем самым позволяет обойтись без просмотра всего списка для определения его последнего элемента. Расцепление можно выполнить также за ограниченное время, если известен индекс компоненты списка, непосредственно предшествующей месту расцепления.

Тривиальной модификацией связанного списка будет следующее, несколько более гибкое представление последовательности: если P_n указывает на S₁ (см. рис. 3.1), то такой список называется циклическим. Это представление даёт возможность достигнуть любого элемента из любого другого элемента последовательности. Включение и исключение элементов здесь осуществляется так же, как и в нециклических списках, в то время как сцепление и расцепление реализуются несколько более сложно.

Еще большая гибкость достигается, если использовать дважды связанный список, когда каждый элемент S_I последовательности вместо одного имеет два связанных с ним указателя на элементы S_i-1 и S_i+1 (рис. 3.4). В таком списке для любого элемента имеется мгновенный прямой доступ к предыдущему и последующему элементам, в связи с чем облегчаются такие операции, как включение нового элемента перед S_i и исключение элемента S_i без предварительного знания его предшественника. Если есть необходи-мость, дважды связанный список очевид-ным образом можно сделать циклическим.

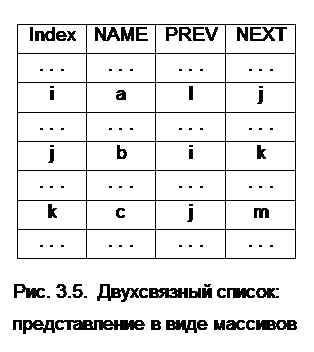Списки можно сделать проходимыми в обоих направлениях, если добавить ещё один массив, называемый PREV (PREVious – предыдущий). Значение PREV[I] равно ячейке, в которой помещается тот элемент списка, который стоит непосредственно перед элементом из ячейки I.

Рассмотрим широко распространённые специального вида списки, с которыми работают ограниченными приёмами: 1) элементы добавляются или удаляются только на одном конце;2)элементы добавляются на одном конце, а удаляются – с другого конца списка. В первом случае доступ к элементам основан на принципе "последний вошёл - первый вышел" (LIFO - Last Input, First Output), и в этом случае список называется стеком, или магазином. Во втором случае доступ к элементам основан на принципе “первый вошёл - первый вышел” (FIFO - First Input, First Output); такого рода список называется очередью.

Первый специального вида список – стек, который обычно реализуется в виде одного массива. Например, список EL1, EL2, EL3 можно хранить в массиве NAME, как показано на рис. 3.6. Переменная TOP (вершина) является указателем последнего элемента, добавленного к стеку.

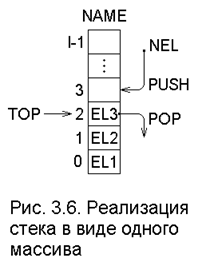Чтобы добавить новый элемент в стек, значение TOP увеличивают на 1, а затем помещают новый элемент в NAME[TOP]. Однако следует иметь в виду, что массив NAME имеет конечную длину l, поэтому перед попыткой вставить новый элемент следует проверить, что TOP< l -1.

Чтобы удалить элемент из вершины стека, надо просто уменьшить значение TOP на 1.

Чтобы узнать, пуст ли стек, достаточно проверить, не имеет ли TOP значение меньше нуля.

Понятно, что время выполнения операций PUSH (ВТОЛКНУТЬ) и POP (ВЫТОЛКНУТЬ) и проверка пустоты стека не зависят от числа элементов в стеке.

Стек обычно используется (например, в микропроцессорах) для хранения адресов возврата при обращении к подпрограммам, а также для запоминания состояния внутренних регистров при обработке прерываний.

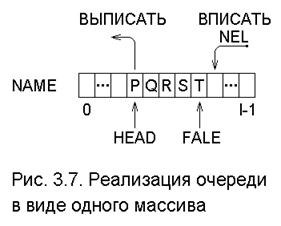Другой специальный вид списка - очередь. Как и стек, очередь можно реализовать одним массивом, как показано на рис. 3.7, где приведена очередь, содержащая список из эле-ментов P, Q, R, S, T. Два указателя обозначают ячейки текущих концов очереди, переднего (HEAD - голова) и заднего (TAIL - хвост). Чтобы добавить (ВПИСАТЬ) новый элемент к очереди, полагают TAIL = TAIL+1 и помещают новый элемент в NAME[TAIL]. Чтобы удалить (ВЫПИСАТЬ) элемент из очереди, заменяют HEAD на HEAD +1.

Так как массив NAME имеет конечную длину (пусть l), указатели HEAD и TAIL рано или поздно доберутся до его конца. Если есть уверенность в том, что длина списка, представленногo этой очередью, никогда не превысит l, то можно трактовать NAME[0] как элемент, следующий за элементом NAME[ l -1]. Другими словами, можно считать этот список кольцевым.

Очередь обычно используется для предварительного анализа команд в конвейере команд (например, в персональных компьютерах) или при организации векторной обработки данных в суперЭВМ.

При работе со списками удаляемые элементы не обязательно физически стирать, однако при этом возникает проблема сбора мусора (ненужных ячеек памяти).

Элементы, расположенные в виде списка, сами могут быть сложными структурами. При работе, например, со списками массивов, на самом деле массивы не добавляются и не удаляются, ибо каждое добавление или удаление потребовало бы времени, пропорционального размеру массива. Вместо этого добавляются или удаляются указатели массивов. Таким образом, сложную структуру можно добавить или удалить за фиксированное время, не зависящее от её размера.

Как было отмечено выше, выбор структуры данных, т. е. способа организации данных в памяти машины, определяется теми операциями, которые будут проводиться над данными.

Рассмотрим основные операции над множествами:

1. Принадлежать (a, S): Если a ÎS, то выдаётся сообщение "да".

2. Вставить (a, S): S ® SÈ{ a }.

3. Удалить (a, S): S ® S{ a }.

4. Найти (a). Сообщается имя того множества, которому в данный момент принадлежит а (если а принадлежит более чем одному множеству, то операция не определена).

5. Объединить (S₁, S₂, S₃): S₃=S₁ÈS₂.

6. Пересечь (S₁, S₂, S₃): S₃=S₁ÇS₂.

7. Сцепить (S₁, S₂, S₃): S₃=S₁. S₂.

8. Расцепить (a, S). Предполагается, что множество S упорядочено отношением 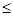. Операция разбивает S на два множества: S₁={ b ï b 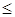a и b ÎS}; S₂={ b ï b > a и b ÎS}.

9. MIN (S). Операция выдаёт наименьший (относительно 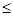) элемент множества S.

10. MAX (S). Операция выдаёт наибольший (относительно 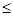) элемент множества S.

Множество в памяти ЭВМ может быть представлено тремя способами: списком, характеристическим вектором и одномерным массивом.

Обычно для представления множеств применяются списки. При этом объём памяти, необходимый для представления множества, пропор-ционален числу его элементов. Время, требуемое для выполнения операций над множествами, зависит от природы операций. Например, пусть А и В - два множества. Операция АВ требует времени, по крайней мере пропорционального сумме размеров этих множеств, поскольку как список, представляющий А, так и список, представляющий В, надо просмотреть хотя бы один раз.

Аналогично операция АÈВ требует времени, пропорционального сумме размеров множеств, поскольку надо выделить элементы, входящие в оба множества, и вычеркнуть каждый экземпляр каждого такого элемента. Если же А и В не пересекаются, можно найти АÈВ за время, не зависящее от размера А и В. Для этого достаточно сделать лишь конкатенацию списков, представляющих А и В. Задача объединения двух непересекающихся множеств усложняется, если необходимо быстро определить, входит ли данный элемент в данное множество.

Рассмотрим представление множества в виде двоичного (битового) вектора. Пусть U - универсальное множество (рассматриваемые множества являются его подмножествами), состоящее из n элементов. Линейно упорядочим его. Подмножество S 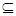U представляется в виде вектора V_s из n битов, такого, что i -й разряд в V_s равен 1 тогда и только тогда, когда i -й элемент множества U принадлежит S. Будем называть V_s характеристическим вектором для S.

Представление в виде двоичного вектора удобно тем, что можно определить принадлежность i -го элемента множества U данному множеству за время, не зависящее от размера данного множества. Более того, основные операции над множествами, такие, как объединение и пересечение, можно осуществлять как операции над двоичными векторами.

Полезность характеристических векторов вытекает из их компактности, существования простого фиксированного соотношения между i и S_i (адресом ячейки и значением i -го разряда вектора) и возможности при таком представлении очень легко добавлять и исключать элементы.

Например, характеристический вектор (ХВ) начального сегмента последовательности простых чисел имеет вид

S_i 1 2 3 4 5 6 7 8 9 10

ХВ для простых чисел 0 1 1 0 1 0 1 0 0 0

Главное неудобство ХВ состоит в том, что они неэкономичны. Исключение составляют "плотные" (в смысле малого числа нулей) подпоследовательности последовательности S₁, S₂, S₃,.... Кроме того, их трудно использовать, если не существует простого соотношения между i и S_i. Если такое соотношение сложное, то использование ХВ может быть очень неэкономичным в смысле времени обработки. Если последовательности недостаточно плотные, то значительным может оказаться объем памяти.

Если операции над двоичными векторами нельзя считать пер-вичными (т. е. выполняемыми за единицу времени), то можно с таким же успехом вместо характеристического вектора определить массив А, для которого А[ i ]=1 тогда и только тогда, когда i -й элемент множества U принадлежит A. При таком представлении все ещё легко выяснить, принадлежит ли данный элемент данному множеству.

Недостаток этого представления в том, что объединение и пересечение занимает время, пропорциональное |U|, а не размерам рассматриваемых множеств. Подобно этому память, требуемая для хранения множества A, пропорциональна |U|, a не |A|.

Дата добавления: 2014-01-14