Графы и их представление

Известно [10] несколько представлений графа G=(V, E), где V – множество вершин, Е - множество ребер. Одно из них - матрица смежностей, т. е. матрица А размера | V |*| V |, состоящая из 0 и 1, в которой A[ i, j ]=1 тогда и только тогда, когда есть дуга из узла i в узел j. Представление в виде матрицы смежности удобно для тех алгоритмов на графах, для которых часто нужно знать, есть ли в графе данная дуга, ибо время, необходимое для определения наличия дуги, фиксировано и не зависит от |V| и |E|.

Основной недостаток применения матрицы смежностей заключается в том, что она занимает память |V|² даже тогда, когда граф содержит только О(|V|) дуг. Уже начальное заполнение матрицы смежностей посредством "естественной" процедуры требует времени О(|V|²), что сводит на нет алгоритмы сложности О(|V|) при работе с графами, содержащими лишь О(|V|) дуг. Поэтому алгоритмы сложности О(|V|), основанные на работе с матрицей смежностей, встречаются редко.

Интересной альтернативой является представление строк и (или) столбцов матрицы смежностей в виде двоичных векторов. Такое представление может способствовать значительной эффективности алгоритмов на графах.

Еще одно представление графа - с помощью списка. Списком смежностей для узла V называется список всех узлов W, смежных с V. Граф можно представить с помощью | V | списков смежностей, по одному для каждого узла.

Пример 3.2. На рис. 3.8,а изображен орграф, содержащий четыре узла, а на рис. 3.8,б - его матрица смежностей. На рис. 3.8,в показаны четыре списка смежностей, по одному для каждого узла. Например, из узла 1 в узлы 2 и 4 идут дуги, так что список смежностей для узла 1 содержит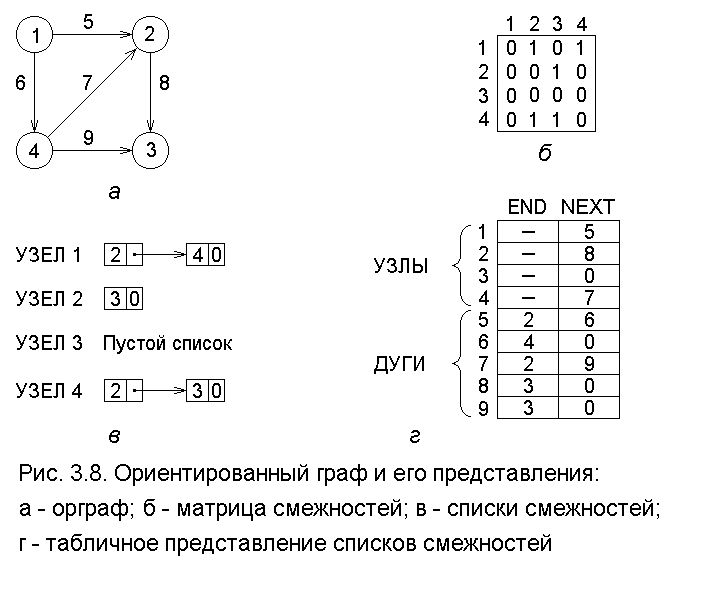
компоненты 2 и 4, связанные в смысле рис. 3.1.

Табличное представление списка смежностей показано на рис. 3.8,г. Каждая из первых четырех ячеек в массиве NEXT содержит указатель на первый узел списка смежностей, а именно NEXT[ i ] указывает на первый узел списка смежностей для узла i.

Заметим, что NEXT[3]=0, поскольку в списке смежностей для узла 3 нет узлов. Остальные составляющие массива NEXT представляют дуги графа. Массив END содержит узлы из списков смежностей. Таким образом, список смежностей узла 1 начинается в ячейке 5, ибо NEXT[1]=5, END[5]=2; это показывает, что есть дуга (1,2). Равенства NEXT[5]=6 и END[6]=4 означают, что есть дуга (1,4), а NEXT[6]=0, что больше нет дуг, начинающихся в узле 1.

Заметим, что представление графа в виде списков смежностей требует памяти порядка |V| + |E|. Таким представлением часто пользуются, если |E|<<|V|².

Если граф неориентирован, то каждое ребро (v,w), т. е. дуга с двумя противоположными направлениями, представляется дважды: один раз в списке смежностей для v и один раз в списке смежностей для w. В этом случае можно добавить новый массив, называемый CON (CONjuction – соединение, связь), чтобы корректировать оба экземпляра неориентированной дуги. Таким образом, если i -я ячейка, соответствующая узлу w в списке смежностей для v, то CON[i]- ячейка, соответствующая узлу v в списке смежностей для w.

Если необходимо с удобством удалять рёбра из неориентирован-ного графа, то списки смежностей можно связать дважды (подразд. 3.1). Это обычно бывает нужно потому, что даже если удалять всегда ребро (v, w), стоящее первым в списке смежностей узла v, всё равно может оказаться, что ребро, идущее в обратном направлении, стоит в середине списка смежностей узла w. Чтобы быстро удалить ребро (v, w) из списка смежностей для w, надо уметь быстро находить ячейку, содержащую предыдущее ребро в этом списке смежностей.

Дата добавления: 2014-01-14