Определения и свойства

Деревья и их представление

Определение. Конечное корневое дерево T - это непустое множество упорядоченных узлов, таких что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы разбиты на m 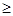0 поддеревьев Т₁,Т₂,...,Т_m. Узлы, не имеющие поддеревьев, называются листьями; остальные узлы называются внутренними.

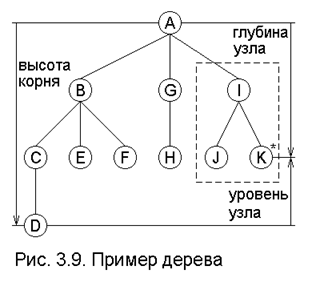
Пример 3.3. На рис. 3.9 изображено дерево с одиннадцатью узлами, помеченными буквами от А до К. Узлы с метками D, E, F, H, J и K являются листьями; другие узлы внутренние. Узел А - корень.

Посредством деревьев изобра-жаются иерархические организации в комбинаторных алгоритмах, поэтому они являются нелинейными структурами данных.

Для описания соотношений меж-ду узлами дерева используется тер-минология, принятая в генеалогиче-ских деревьях.

Так, в дереве (или поддереве) все узлы являются потомками его корня, и наоборот, корень - предок всех своих потомков. Корень именуется отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. На рис. 3.9 узел А является отцом узлов B, G и I; J и K - сыновья I, а C, E, F - братья; пунктиром выделено поддерево с узлами I, J, K.

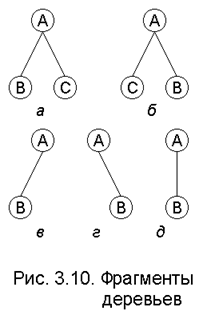
Все рассматриваемые деревья будут упорядочены, т.е. для них будет важен относительный порядок расположения следования каждого узла. Таким образом, деревья, представленные на рис. 3.10,а и б, счи-таются различными.

Для дерева вводятся следующие характеристики:

· глубина узла v в дереве - это длина пути из корня в v;

· высота узла в дереве - это длина самого длинного пути из v в какой-нибудь лист;

· высотой дерева называется высота его корня;

· уровень узла v в дереве равен разности высоты дерева и глубины узла v.

Например, на рис. 3.9 высота дерева равна 3; узел К имеет глубину 2, высоту 0 и уровень 1.

Определение. Лес - упорядоченное множество деревьев. В связи с этим можно переопределить понятие дерева: дерево есть непустое множество узлов, такое, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы образуют лес с m 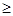0 поддеревьями корня.

Важной разновидностью корневых деревьев является класс бинарных (двоичных) деревьев.

Определение. Бинарное дерево Т либо пустое, либо состоит из выделенного узла, называемого кор-нем, и двух бинарных поддеревьев: левого Т₁ и правого T₂. Бинарные деревья не являются подмножеством множе-ства деревьев, они полностью отличаются по своей структуре, поскольку две следующие картинки (в и г на рис. 3.10) не изображают одно и то же бинарное дерево. Как деревья, однако, они обе неотличимы от картинки д.

Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, и каждый узел дерева может иметь произвольное число поддеревьев; в то же время бинарное дерево может быть пустым, каждый из его узлов может иметь 0, 1 или 2 поддерева, и существует различие между левыми и правыми поддеревьями.

Определение. Бинарное дерево называется полным, если для некоторого целого k каждый узел глубины меньше k имеет как левого, так и правого сына, а каждый узел глубины k является листом. Полное бинарное дерево высоты k имеет ровно 2 ^{k +1}–1 узлов.

Определение. Неориентированным деревом называется неориен-тированный ациклический связанный (любые два узла соединены путем) граф. Корневое неориентированное дерево - это неориентированное дерево, в котором узел выделен в качестве корня.

Ориентированное дерево можно превратить в корневое неориен-тированное, просто сделав все его ребра неориентированными. Обычно используют одну и ту же терминологию и применяют одни и те же обоз-начения для корневых неориентированных и ориентированных деревьев. Основное математическое различие здесь состоит в том, что все пути в ориентированном дереве идут от предков к потомкам, тогда как в корне-вом неориентированном дереве пути могут идти в обоих направлениях.

Дата добавления: 2014-01-14