Примеры. 1. Рассмотрим задачу нахождения корней многочленов вида ,

1. Рассмотрим задачу нахождения корней многочленов вида 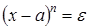, 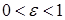. Изменение правой части на величину порядка e приводит к погрешности корней порядка 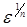, что при больших n гораздо больше e. Например, если правую часть уравнения 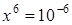увеличить на 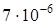, то есть рассмотреть уравнение 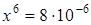, то корень увеличится примерно на 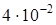(с 0,10 до 0,14).

2. Пример Уилкинсона. Рассмотрим многочлен

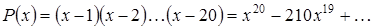
Очевидно, что корнями многочлена являются 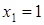, , 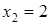…, 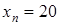. Предположим, что один из коэффициентов многочлена вычислен с некоторой малой погрешностью. Например, коэффициент 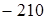при 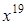увеличим на 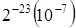. В результате вычислений с точностью до 11 значащих цифр получим существенно другие значения корней, и половина корней станет мнимыми. Причина такого явления – неустойчивость самой задачи, так как вычисления выполнялись очень точно (11 разрядов) и погрешность округлений не могла привести к таким результатам.

Задача называется поставленной корректно, если для всех значений исходных данных из некоторого класса ее решение существует, единственно и устойчиво по исходным данным. Рассмотренные выше примеры неустойчивых задач является некорректно поставленными. Применять для решения таких задач численные методы, как правило, нецелесообразно, так как возникающие в расчетах погрешности округлений будут сильно возрастать в ходе вычислений, что приведет к значительному искажению результатов.

Однако в настоящее время разработаны методы решения некоторых некорректных задач. Это, в основном, так называемые методы регуляризации, которые основываются на замене исходной задачи корректно поставленной задачей.

При анализе точности вычислений процесса одной из важнейших характеристик является сходимость численного метода. Она означает близость получаемого численного решения задачи к исходному решению. Различают сходимость итерационного процесса и сходимость в методах дискретизации.

Рассмотрим понятие сходимости итерационного процесса. Этот процесс состоит в том, что для решения некоторой задачи строится метод последовательных приближений. В результате многократного повторения этого процесса (итераций) получаем последовательность значений 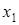, , 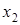…, , …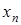. Говорят, что эта последовательность сходится к точному значению 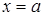, если при неограниченном возрастании числа итераций предел этой последовательности существует и равен a. То есть 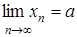. В этом случае имеем сходящийся численный метод. (Например, метод Ньютона для численного решения уравнений.)

Рассмотрим теперь понятие сходимости, используемое в методах дискретизации. Эти методы заключаются в замене задачи с непрерывными параметрами на задачу, в которой значения функции вычисляются в фиксированных точках. Здесь под сходимостью понимается стремление значений решения дискретной модели к соответствующим значениям решения исходной задачи при стремлении к нулю параметра дискретизации. (Например, квадратурные формулы.)

При рассмотрении сходимости важными понятиями являются вид сходимости, ее порядок и другие характеристики. В общем виде эти понятия рассматривать нецелесообразно, мы будем обращаться к ним при изучении конкретного численного метода.

Таким образом, для получения решения задачи с некоторой точностью ее постановка должна быть корректной, а используемый численный метод должен обладать сходимостью.

Дата добавления: 2014-01-14