Лекция 4. «О вычитании «близких чисел»

«О вычитании «близких чисел».

Обратная задача теории приближенных вычислений.

О вычислениях без строгого учета погрешностей.»

О вычитании «близких чисел».

Пусть даны при­ближенные числа и , требуется найти их разность. Находим: . Заметим, что , то есть относительные погреш­ности данных чисел очень малы. Найдем теперь относительную погрешность разности.

.

Как видим, относительная погрешность разности почти в 5000 раз больше, чем погрешность вы­читаемого и уменьшаемого. Говорят, что при вычитании близких чисел происхо­дит потеря точности.

Точность результата при вычитании близких чисел можно повысить, если перед выполнением вычислений произвести тождественные преобразования так, чтобы избежать вычитания близких чисел. Например, пусть (под знаком радикала стоят точные числа). Это разность близких чисел. Во избежание потери точ­ности преобразуем выражение так:

.

Относительная погрешность этого приближения равна: . Если бы мы не проводили тождественных преобразований, то: , !

Обратная задача теории приближенных вычисле­ний.

Рассмотрим задачу. Требуется вычислить объем ко­нуса по формуле так, чтобы погрешность не превышала 1%. С какой точностью следует измерить радиус основания и высоту, чтобы обеспечить требуемую точность результата?

Для решения задачи следует знать грубые прибли­женные значения R и Н по недостатку. Пусть (); (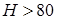). На основании теоремы об умножении приближенных чисел составляем неравенство: . Число p мы можем взять с любой степенью точности, то есть 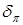можно взять сколь угодно малым. Положим пока, , то есть . Неравенство будет таково: 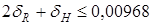. Мы получили одно неравенство с двумя неизвестными. Но мы можем наложить на и некоторые допол­нительные условия. Например, мы можем считать, что измерения R и Н будут проведены при одинаковой точности измерительных инструментов. Значит, можно поло­жить . Так как

(), (),

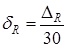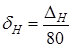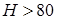то находим: . Отсюда . Значит, для получения требуемой точности достаточно произвести измерения R и Н с погрешностью, не превышающей 1 мм, так как

.

Итак, в теории приближенных вычислений рассматри­ваются две основные задачи.

Прямая задача. Указаны действия, которые следует выполнить над приближенными числами (например, про­извести вычисления по данной формуле), и заданы предельные погрешности этих чисел. Требуется оценить погреш­ность результата.

Обратная задача. Указаны действия, которые нужно выполнить над приближенными числами (например, про­вести вычисления по данной формуле). Требуется установить, каковы должны быть допустимые погрешности при­ближенных чисел, чтобы полученный результат имел наперед заданную предельную погрешность.

Дата добавления: 2014-01-14