Постановка задачи. Численные методы решения уравнений

Лекция 5.

Численные методы решения уравнений.

Правила верных цифр.

О вычислениях без строгого учета погрешностей.

Приведенные теоремы позволяют проводить строгий учет погрешности. Применяя, например, теорему о сложении приближенных чисел, мы можем гарантировать, что при вычислении суммы 10 слагаемых, каждое из которых имеет абсолютную погрешность, не превышающую 0,005, погреш­ность суммы не превзойдет 0,05. Однако найденная таким образом граница погрешности обычно бывает значительно завышенной, она получается с большим «запасом». В дейст­вительности при сложении 10 слагаемых погрешность возрастает (в большинстве случаев) не в 10 раз, а лишь немного превышает погрешность слагаемых. Поэтому при выполнении арифметических действий над приближенными числами в тех случаях, когда не требуется строгого учета точности, установлены правила, позволяющие быстро, без громоздких исследований определить, как нужно проводить вычисления, чтобы получить результат нужной точности. Эти правила не столь точны, как правила вычислений со строгим учетом погрешностей, но во многих вычислениях вполне достаточны. Они называются правилами верных цифр. При формулировке этих правил будем считать, что число данных чисел невелико.

1. При сложении и вычитании приближенных чисел в результате младший сохраненный десятичный разряд должен быть тот, который соответст­вует наименее точному из слагаемых. (Например: 2,173+1,22=3,393=3,39.)

2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет при­ближенное данное с наименьшим числом значащих цифр. (Например: 3000×0,21=6,3×10².)

3. При возведении в квадрат и куб в результате следует сохранять столько значащих цифр, сколько их имеет воз­водимое в степень приближенное число.

4. При извлечении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их имеет приближенное значение подкоренного числа.

5. При вычислениях по формуле во всех промежуточных результатах следует сохранять одной цифрой больше, чем рекомендуют предыдущие правила. В окончательном ре­зультате эта «запасная» цифра отбрасывается.

6. Если какое-нибудь данное имеет больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то его предварительно следует округлить, сохраняя одну лишнюю цифру.

Глава 2.

«Постановка задачи. Метод половинного деления.»

Пусть задана некоторая функция , являющаяся левой частью уравнения .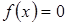

Задача решения уравнения 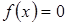заключается в отыскании такого значения , где X – область определения 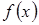, что . Ясно, что аналитическое, или как принято говорить «точное» решение уравнения 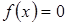возможно получить лишь, когда удается аналитически представить 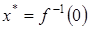, где 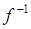– обратная для функция.

В общем случае задача решается с использованием специально разработанных методов, позволяющих отыскивать некоторое приближение для 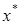с гарантированной погрешностью. При этом, как правило, исходная задача сводится к решению двух последовательных задач: задаче локализации (отделения) корня и задаче уточнения корня.

Рассмотрим каждую из задач более подробно. Задача локализации (отделения) корня уравнения состоит в следующем: найти отрезок, содержащий единственный корень уравнения 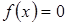. В основе аналитического способа отделения корней лежит следующая теорема существования.

Теорема 2.1. (Теорема Коши.) Если и , то существует точка такая, что.

Идея метода заключается в том, что исходный отрезок 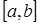разбивается на n частей – элементарных отрезков и в каждом отрезке исследуется знак функции на его концах.

Теорема Коши не гарантирует единственности корня. Единственность корня следует из монотонности функции на отрезке . То есть справедлива следующая теорема единственности.

Теорема 2.2. Если существует точка такая, чтои 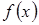монотонна на отрезке , то 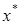– единственный корень на отрезке .

На практике при аналитическом отделении корней шаг разбиения отрезка берут достаточно малым.

Кроме аналитического отделения корней существует и графический способ, основанный на построении качественного графика функции 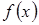и приближенного (на глаз) определения точек пересечения графика с осью Ox. Если график функции 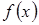построить трудно, то представляют уравнение в виде . И тогда решением уравнения будут абсциссы точек пересечения графиков и .

Пример. .

Рис. 2.1.

Задача уточнения корней заключается в том, чтобы найти точку такую, что , где 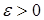– заданная точность решения уравнения .

Дата добавления: 2014-01-14