Вычисление значений многочленов

Очень часто в качестве аппроксимирующей функции берут многочлен. Это связано с тем, что множество многочленов всюду плотно во множестве непрерывных функций. То есть имеет место следующая теорема.

Теорема 4.1. (Теорема Вейерштрасса.) Если 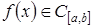, то для любого 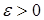существует многочлен такой, что при всех .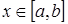

Кроме того, и это немаловажно, значения многочлена легко вычисляются. Рассмотрим алгебраический многочлен

,

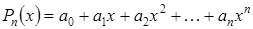где , , 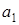…, 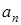– числовые коэффициенты, n – степень многочлена. Если проводить вычисления в «лоб», то есть находить значения каждого члена и суммировать их, то при больших n потребуется выполнить большое число операций: 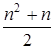умножений и n сложений. Кроме того, это может привести к потере точности за счет погрешности округлений.

Запишем многочлен в следующем виде:

.

Согласно этой формуле вычисление значения сводится к последовательному нахождению следующих величин:

;

;

;

…

;

.

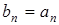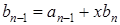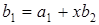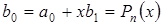Способ нахождения значения многочлена по вышеописанным формулам называется схемой Горнера. Для реализации этой схемы требуется n умножений и n сложений, то есть всего 2n арифметических действий. Схема Горнера является в общем случае самым оптимальным способом вычисления значения многочлена. Использование этой схемы не только экономит машинное время, но и повышает точность вычислений за счет уменьшения погрешности округления. Схема Горнера удобна также для реализации на ЭВМ благодаря цикличности вычислений и необходимости сохранять кроме коэффициентов многочлена и значения аргумента только одно значение промежуточной величины, а именно при текущем .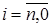

Дата добавления: 2014-01-14