Остаточный член интерполирования

Пусть 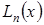– интерполяционный многочлен, построенный для функции по узлам 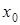, , 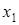…, 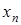. В узлах значения 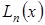и равны между собой. В точках x, не совпадающих с узлами, вообще говоря, . Всегда можно написать равенство , где - остаточный член, то есть погрешность интерполяции, которая характеризует точность приближения функции интерполяционным многочленом .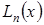

Заметим, что если относительно функции ничего не известно, кроме её значений в узлах интерполяции, то никаких полезных рассуждений относительно остаточного члена провести нельзя. В предположении, что 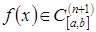, где 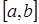– отрезок, содержащий все узлы интерполяции 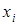, , например, , , можно оценить погрешность интерполяции. Оценим остаточный член в произвольной точке 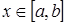, не совпадающей ни с одним из узлов. Имеет место следующая теорема об остаточном члене интерполирования.

Теорема 4.3. Если 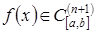, то для всякого 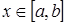найдется точка 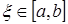такая, что

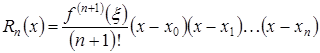. (4.3)

Доказательство.

Рассмотрим функцию

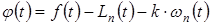, (4.4)

где k – некоторое число, , .

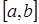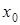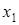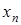Очевидно, что имеет на производные до порядка включительно. Узлы , , …, являются корнями . Возьмем произвольную точку 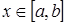, не совпадающую ни с одним из узлов, и подберем k так, чтобы .

Полагая в (4.4) 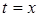и , получим, что k следует взять равным

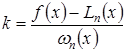. (4.5)

При этом значении k функция обращается в нуль в (n+2) точках x, 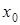, , 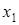…, 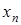. В анализе доказывается теорема Ролля: если функция непрерывна на и дифференцируема на 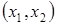и на концах отрезка принимает равные значения, то существует хотя бы одна точка 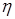внутри отрезка , в которой производная .

Применяя эту теорему к функции , получаем, что её производная обращается в нуль по крайней мере в (n+1) точках отрезка 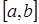. Вновь применяя теорему Ролля, но уже к функции 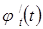, получаем, что производная функции 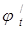обращается в нуль по крайней мере в n точках отрезка 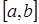. Продолжая эти рассуждения дальше, имеем, что обращается в нуль по крайней мере в одной точке. Обозначим ее через . Отметим, что (n+1)-я производная , то есть 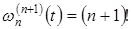, так как 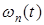есть многочлен степени 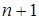со старшим коэффициентом 1.

Из 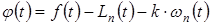имеем . Полагая в этом равенстве и учитывая, что , находим .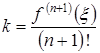

Подставив найденное значение k в формулу (4.5), найдем

.

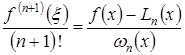Откуда

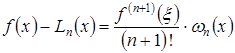
или

.

Теорема доказана.

Если 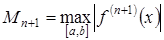, то

. (4.6)

Это и есть оценка погрешности интерполяции.

Дата добавления: 2014-01-14