Многочлены Чебышева

Минимизация оценки погрешности интерполяции.

Многочлены Чебышева.

Лекция 14.

«Минимизация оценки погрешности интерполяции.

Локальная интерполяция. Сплайны.»

Поставим перед собой проблему оптимизировать оценку (4.6), то есть попытаемся сделать такой выбор узлов 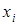, чтобы был минимальным.

Рассмотрим отрезок 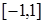. Для задачи минимизации понадобятся многочлены Чебышева.

Определение 4.1. Многочленом Чебышева при называется следующая функция .

Очевидно, что 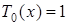, . Остальные многочлены Чебышева можно получить по следующему рекуррентному соотношению:

, (4.7)

где . Действительно, используя формулы косинуса суммы и разности, получаем:

.

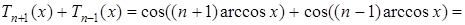
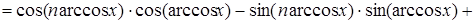
Тогда 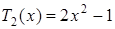, и так далее.

Укажем свойства многочленов Чебышева.

1. – многочлен степени n на 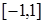; 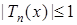. При четном (нечетном) n многочлен содержит только четные (нечетные) степени x. (Это следует из формулы (4.7).)

2. Старший коэффициент равен ().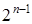

3. На отрезке 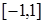имеет ровно n корней, которые имеют вид

, .

Действительно,

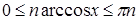Û[, так как ]Û

Û.

4. На отрезке 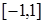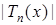принимает максимальное значение 1 ровно в (n +1) точке, которые имеют вид , .

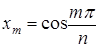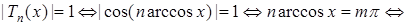
Û[, так как ]Û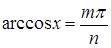

Û() Û ().

Отметим также, что

,

а, следовательно, знаки многочлена в точках 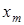чередуются. Таким образом, .

5. Обозначим через 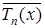многочлен, который получается из многочлена Чебышева нормированием, то есть приведением к виду, в котором старший коэффициент равен 1. Тогда .

Докажем, что многочлен 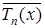имеет на отрезке 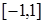наименьшее значение максимума модуля среди всех многочленов n -ой степени со старшим коэффициентом 1. Допустим противное, то есть что существует многочлен 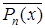степени n со старшим коэффициентом 1, причем

. (4.8)

Рассмотрим разность . Это многочлен степени не выше, чем . По свойству 4 многочленов Чебышева и благодаря (4.8) эта разность на отрезке 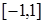имеет (n +1) значение с чередующимися знаками в точках 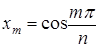, . Следовательно, функция по крайней мере в n точках имеет значение, равное нулю. Итак, многочлен степени не выше, чем (), имеет n корней. Полученное противоречие доказывает свойство 5.

Построим графики первых четырех многочленов Чебышева. Они иллюстрируют свойства этих многочленов.

Рис. 4.1.

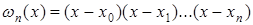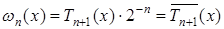Возьмем в качестве узлов интерполяции корни многочлена . Тогда многочлен будет пропорционален , причем он получается из следующим образом: . В этом случае оценка погрешности интерполяции будет выглядеть так:

.

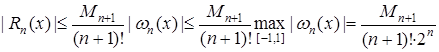Так как 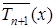имеет на отрезке 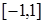наименьшее значение максимума модуля, то вышеуказанную оценку за счет другого выбора узлов интерполяции улучшить невозможно.

В случае произвольного отрезка 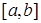нужно преобразовать отрезок 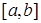в отрезок 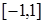и в качестве узлов интерполяции 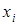взять точки, соответствующие корням многочлена Чебышева на отрезке .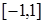

, , .

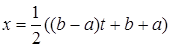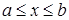В качестве узлов интерполяции выбираем точки

.

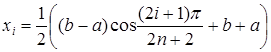Дата добавления: 2014-01-14