Отображение РС-кодов над GF(2m) на двоичные коды

Элементы GF (q) при q = p^m, как это было рассмотрено выше, могут быть представлены последовательностями длины m с элементами из GF (p). В этом случае (N, K)-код РС с расстоянием D над GF (q) становится (n = mN, k = mK)-кодом над GF (p) с расстоянием d ³ D.

Если q= 2 ^m, то двоичные коды, получаемые таким путем, часто имеют большое минимальное расстояние.

Пусть ξ₁, …, ξ _m –базис элементов поля GF (2 ^m) над GF (2). Тогда, если 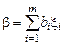– произвольный элемент GF (2 ^m), где b_i=GF (2), то β отображается в последовательность длины m:
b ₁, b ₂, …, b_m.

Это отображение переводит линейные коды в линейные. При этом циклические коды не обязательно переходят в циклические.

Пример 7.5

Используя базис 1, α для элементов GF (4) над GF (2), получаем отображение 0®00, 1®10, α®01, α²®11. Тогда РС-код (3,2) с D =2 над полем GF (4) примера 5.13 становится двоичным (6,4)-кодом с d= 2, приведенным ниже:

0. 000000 4. 000110 8. 001101 12. 001011

1. 011000 5. 011110 9. 010101 13. 010011

2. 110100 6. 110010 10. 111001 14. 111111

3. 101100 7. 101010 11. 100001 15. 100111

Легко проверить, что данный код не является циклическим.

Пример 7.6

Рассмотрим (7,5) – РС-код над GF (2³) с D = 3 [3]. Поле GF (2³), построенное по модулю П(α)=α+α³+1, содержит следующие элементы:

0 0 0 =0, 1 0 0= 1, 0 1 0 =α, 0 0 1 =α²,

1 1 0 =α³, 0 1 1 =α⁴, 1 1 1 =α ⁵, 1 0 1 =α⁶.

В качестве базиса для элементов GF (2³) над GF (2) возьмем 1,α,α⁶,

т.е. β = b ₁(100)+ b ₂(010)+ b ₃(101).

Тогда получим отображение 0®000, 1®100, α®010, α²®101, α³®110,α ⁴®111,α⁵®011,

α⁶®001.

Сформируем порождающий многочлен в виде

g (x)=(x +α⁵)(x +α⁶)=α⁴+αx+ x ².

При таком построении РС-код (7,5) с= D= 3 переходит в двоичный циклический код (21,15) с порождающим многочленом g (x)=1+ x + x ²+ x ⁴+ x ⁶и минимальным расстоянием d= 3. Это единственный известный нетривиальный пример РС-кода, отображаемого в двоичный циклический код.

Способы кодирования и декодирования РС-кодов достаточно хорошо разработаны в теоретическом и реализационном плане. Их основу составляют процедуры исправления стираний, ошибок и совместного исправления ошибок и стираний. Рассмотрим процедуры, нашедшие применение в отечественной технике передачи данных.

Рассмотрим процедуру декодирования с исправлением ошибок, известную [ 4 ] как алгоритм Форни.

Пусть в приемник аппаратуры передачи данных (АПД) поступила кодовая комбинация РС-кода

C (x)= f (x)+ e (x),

где f (x) – переданная передатчиком (АПД) кодовая комбинация, в которой в процессе передачи по каналу связи произошло v ошибок, отображаемых многочленом e (x) степени u. Каждый ненулевой компонент e (x) описывается парой элементов: Y_i – величина ошибок и X_i – номер позиции ошибки (локатор ошибки). Y_i, X_i – элементы GF (q), и элемент X_i=αⁱ,αⁱ Є GF(q).

Для описания ошибок используются:

1. Многочлен локаторов ошибок:

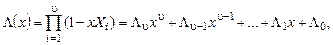
имеющий корни X_i ^–1, i = 1, …,v взаимные к локаторам ошибок, т. е. X_i ^–1∙α ⁱ = 1.

2. Многочлен значений ошибок :

Ω(x)= S (x)Λ(x) (mod x ^{2 t}), (*)

где – синдромный многочлен бесконечной степени, для которого известны только 2 t коэффициентов для поступившей комбинации РС-кода.

Здесь – элемент синдрома, α j – корень порождающего многочлена РС-кода. Значения S_j = e (α ^j) задаются проверками:

S_j=C(α^j)=f(α^j)+e(α^j)=e(α^j),

где m ₀£ j £ m ₀+2 t –1 при m ₀=1.

Равенство (*) определяет множество из (2 t –υ) уравнений и называется ключевым уравнением, так как оно представляется «ключом» решения задачи декодирования.

Это становится понятным, если учесть, что степень Ω(x) не превышает υ–1 и поэтому справедливо:

,

где .

Из (*) необходимо получить υ уравнений для υ неизвестных коэффициентов Λ_k. Эти уравнения являются линейными. Они могут быть решены обычными методами либо с помощью итерационных процедур. После нахождения многочлена Λ(x) ключевое уравнение позволяет найти неизвестные компоненты вектора e (x) и по ним выходной вектор декодера: f (x)= C (x)+ e (x).

Простейшим путем нахождения корней многочлена Λ(x) является метод проб и ошибок, известный как процедура Ченя. Эта процедура состоит в последовательном вычислении Λ(α^j) для каждого j и проверки полученных значений на ноль. Если величина Λ(α^–k) равна нулю, то α^k является взаимным к корню многочлена локаторов ошибок и k -й элемент кодовой комбинации содержит ошибку. Наиболее простым способом вычисления значения Λ(x) в точке β является схема Горнера:

.

Для вычисления Λ(β) по схеме Горнера требуется только υ умножений и υ сложений, где υ – степень Λ(x).

После определения локаторов ошибок с помощью ключевого уравнения находим значения ошибок. Для этого, используя значения сомножителей, входящих в равенство для Ω(x), перепишем ключевое уравнение следующим образом:

Сворачивая выражение в квадратных скобках, получаем окончательно

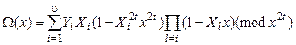
Приводя это выражение по модулю x ^{2 t}, получаем

.

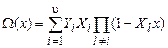Вычислим многочлен значений ошибок на позиции l: .

,

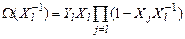откуда

.

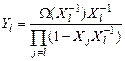Найдем производную от многочлена локаторов ошибок Λ(x):

.

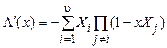Для l -й позиции получаем:

.

С учетом последнего выражения Y_l значение ошибки на позиции l принимает вид

.

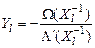Рассмотренный способ декодирования позволяет найти значение ошибок по известным многочленам локаторов и значений ошибок. Он известен в литературе [ 4 ] как алгоритм Форни. Указанные многочлены вычисляются в результате решения ключевого уравнения.

Дата добавления: 2014-01-14