Относительность движения

График скорости.

Графическое представление движения

Скорость.

Прямолинейное равномерное движение.

Тема 1.1.2

Прямолинейное движение — это движение, при котором траектория тела (точки) —прямая линия. Примером может служить движение автомобиля по участку дороги, на котором нет подъемов, спусков, поворотов. А прямолинейным равномерным движением называют такое движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения.

Для описания прямолинейного движения удобно направить одну из координатных осей, например ось X, вдоль той прямой, по которой движется тело. Тогда координата х будет единственной координатой, которая изменяется при движении. Вектор перемещения при таком выборе оси может быть направлен либо так же, как координатная ось, либо противоположно ей В первом случае проекция s_x вектора s₂ положительна и равна модулю вектора: s_2x = s₂ Во втором она отрицательна и равна S₃x= —S₃.

V= s: t

Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению перемещения тела за любой промежуток времени к значению этого промежутка.

Зная скорость v, мы найдем и перемещение за любой промежуток времени t:

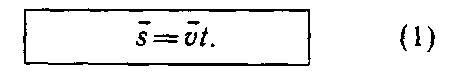
Направлен вектор скорости так же, как вектор перемещения. Направление вектора скорости — это и есть направление движения тела.

Как изменяется положение движущегося тела со временем?

При вычислениях перемещения и скорости пользуются формулами, в

которые входят не векторы, а их проекции на оси (или ось) координат. Проекции векторов — величины скалярные, поэтому над ними можно производить алгебраические действия. Так как векторы s и vt равны, то равны и их проекции на ось X. Поэтому формула (1а) в скалярной форме записывается так:

1К1 (6.09)

Теперь, используя формулы 1а и 2аи (1), можно вычислить координату х тела в любой момент времени t:

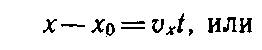
х = х₀+ v_хt 3С-1 (6.09.11 Опрос) (2)

Таким образом, мы нашли, как координата х тела зависит от времени t. А это и есть решение основной задачи механики.

Формулу (2) можно использовать и для того, чтобы вычислить проекцию скорости v_x тела, если нам известна проекция s_x перемещения:

Эта формула позволяет понять, какой смысл имеет величина «скорость». Из нее видно, что проекция скорости на координатную ось равна изменению координаты в единицу времени, т. е. скорость показывает, как быстро изменяются при движении координаты тела. Но при этом необходимо помнить, что проекция скорости v_x может быть как положительной, так и отрицательной (рис. 23 и 24).

Дата добавления: 2014-01-14