Работа силы упругости

Вопросы

1. Как связана потенциальная энергия тела с работой силы тяжести?

2. Как изменяется потенциальная энергия тела при его движении вверх?

3. Изменяется ли потенциальная энер­гия при движении тела параллельно по­верхности Земли?

4.Что такое нулевой уровень?

Упражнение 25

1. Груз массой 2,5 кг падает с высоты 10 м. На сколько изменится его потен­циальная энергия через 1 с после начала падения? Начальная скорость груза равна нулю.

2. Какая работа совершается силой тя­жести, когда человек массой 75 кг подни­мается по лестнице от входа в дом до 6-го этажа, если высота каждого этажа 3 м?

3. Перепад высот между местами старта и финиша горнолыжных соревнований составляет 400 м. Слаломист принимает старт и благополучно финиширует. Чему равна работа силы тяжести, если масса слало­миста перед стартом равна 70 кг?

4. Место финиша трассы горнолыжных соревнований находится на высоте 2000 м над уровнем моря, а точка старта — на высоте 400 м над точкой финиша. Чему равна потенциальная энергия лыжника на старте относительно точки финиша и уров­ня моря? Масса лыжника 70 кг.

Сила упругости — это сила, воз­никающая при деформации тела. В качестве примера силы упругости удобно рассматривать силу упру­гости пружины, хотя все законо­мерности, установленные для пру­жины, относятся и к другим дефор­мированным телам. Сила упругости пропорциональна деформации, в частности удлинению пружины. На­правлена она в сторону, противо­положную смещению частиц тела при деформации.

На рисунке 141, а показана пружина в ее естественном, недеформированном состоянии. Правый конец пружины закреплен, а к ле­вому прикреплено какое-то тело. Направим ось координат X так, как показано на рисунке. Если пружину сжать, сместив ее левый конец впра­во на расстояние Х₁, то возникает сила упругости (рис. 141,6), направ­ленная влево. Проекция этой силы на ось X равна — kx₁, где k — жест­кость пружины.

Предоставим теперь пружину самой себе. Тогда конец пружины будет смещаться влево. При этом движении сила упругости совершает работу.

Предположим, что левый конец пружины (и тело, скрепленное с ним) переместился из положения А в по­ложение В (рис. 141, в). В этом положении деформация (удлинение) пружины равна уже не х₁, а х₂. Перемещение конца пружины равно разности координат конца пружины:

Х₁— Х₂.

Направления силы и перемеще­ния совпадают, и чтобы найти ра­боту, нужно перемножить модули силы упругости и перемещения. Но сила упругости при движении изме­няется от точки к точке, потому что изменяется удлинение пружины: в точке А модуль силы упругости равен kx₁, в точке В — kx₂. Для вы­числения работы силы упругости нужно взять среднее значение силы упругости и умножить его на пере­мещение:

A = F_cp(x₁—x₂).

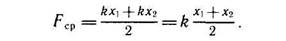
Подставим это значение средней силы в формулу для работы:

Среднее значение силы упругос­ти равно полусумме начального и конечного ее значений:

(x₁ - x₂)

Так как (x_l + x₂)(x₁—x₂) = x²₁ — х₂², то работа получается равной

Работа, как видно из этой фор­мулы, зависит только от координат x₁ и x₂ начального и конечного по­ложений конца пружины (x₁ и x₂ — это и удлинения пружины, и коор­динаты ее конца).

Интересно, что в формулу для работы не входит масса тела, при­крепленного к пружине. Но и сила упругости от массы тела, к которому она приложена, не зависит. Уже ранее указывалось, что в этом со­стоит особенность силы упругости.

Потенциальная энергия дефор­мированного тела.

Формулу (1) для работы силы упругости можно за­писать (переставив порядок членов в правой части) в таком виде:

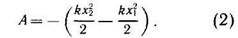
Здесь в правой части равенства

kx²

стоит изменение величины —2- со знаком «минус».

В предыдущем параграфе вели­чину mgh, изменение которой (с противоположным знаком) равно ра­боте силы тяжести, мы назвали по­тенциальной энергией поднятого те­ла. Такое же название можно дать и

величине kx²/2, раз ее изменение, и тоже с противоположным знаком, равно работе. Величина kx²/2 пред­ставляет собой потенциальную энер­гию деформированного тела, в част­ности пружины.

Формула (2) означает, что ра­бота силы упругости равна изме­нению потенциальной энергии уп­руго деформированного тела (пру­жины), взятому с противоположным знаком.

Работа силы упругости, как и работа силы тяжести, зависит толь­ко от начальной и конечной коор­динат свободного конца, например, пружины (от х₁ до х₂). Поэтому о ней можно сказать то же, что и о ра­боте силы тяжести,— эта работа не зависит от формы траектории. А если траектория замкнутая, то ра­бота равна нулю.

Если за начало отсчета коор­динаты принять положение конца недеформированной пружины, а пру­жина удлинена на х, то формула (2) принимает вид:

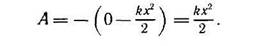
Но kx²/2 это потенциальная энер­гия тела (пружины) при удлине­нии х. Значит, потенциальная энер­гия деформированного тела равна работе силы упругости при пере­ходе тела (пружины) в состояние, в котором его деформация равна нулю. О потенциальной энергии тела, на которое действует сила тяжести, мы говорили, что это энергия взаи­модействия. Потенциальная энергия упруго деформированного тела — это тоже энергия взаимодействия. Но теперь это энергия взаимодейст­вия частиц, из которых состоит тело. Это относится и к пружине. В ней взаимодействуют витки пружины, частицы вещества, из которых она сделана.

Вопросы

1. Чему равно среднее значение силы упругости?

2. В чем сходство выражений для ра­боты силы упругости и работы силы тя­жести?

3. Чему равна работа силы упругости, если тело, на которое она действует, пройдя какое-то расстояние, вернулось в исходную точку?

4. Может ли обладать потенциальной энергией тело, находящееся в состоянии равновесия?

5. Может ли обладать потенциальной энергией тело, на которое не действуют никакие силы?

6. Чему равна потенциальная энергия уп­руго деформированного тела?

7. Что общего у потенциальных энер­гий деформированного тела и тела, на ко­торое действует сила тяжести?

Упражнение 26

1.Мальчик определил, что максимальная сила, с которой он может растягивать ди­намометр, равна 400 Н. Чему равна работа этой силы при растяжении динамометра? Жесткость пружины динамометра равна 10 000 Н/м.

2.К пружине, верхний конец которой закреплен, подвешено тело массой 18 кг. При этом длина пружины равна 10 см. Когда же к ней подвешено тело массой 30 кг, ее длина равна 12 см. Вычислите работу, которую совершает внешняя сила при растяжении пружины от 10 до 15 см. Какую работу совершает при этом сила упругости?

3. На рисунке 142 показан график за­висимости силы упругости, возникающей при сжатии пружины, от ее деформации. Вы­числите, используя этот график, работу внешней силы при сжатии пружины на 2 см. Докажите, что эта работа численно равна площади треугольника АОВ.

4. Имеются две пружины с одинаковой жесткостью. Одна из них сжата на 5 см, другая растянута на 5 см. Чем разли­чаются удлинения этих пружин и их потен­циальные энергии?

5. К пружинным весам подвешен груз. При этом груз опустился и стрелка весов остановилась на цифре 3. На сколько уве­личилась потенциальная энергия пружины весов, если шкала весов градуирована в ньютонах, а расстояние между соседними делениями равно 5 мм!

5. Сжатая пружина, жесткость кото­рой 10 000 Н/м, действует на прикреплен­ное к ней тело с силой 400 Н. Чему равна потенциальная энергия пружины? Какая ра­бота была совершена внешней силой при ее сжатии? Какую работу совершит сила уп­ругости пружины, если дать ей возможность восстановить первоначальную форму?

Рис. 142

Дата добавления: 2014-01-14