Построение уравнений движения

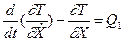
или раскрывая полную производную:

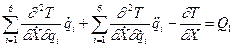
Для всех шести уравнений следует производить дифференцирование, аналогично первому уравнению.

Уравнения движения представляют систему линейных дифференциальных уравнений 2-го порядка следующего вида:

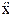
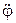
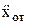
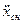
№п/п							B
	m11	m12	m13	m14	m15	m16	=b1
	m21	m22	m23	m24	m25	m26	=b2
	m31	m32	m33	m34	m35	m36	=b3
	m41	m42	m43	m44	m45	m46	=b4
	m51	m52	m53	m54	m55	m56	=b5
	m61	m62	m63	m64	m65	m66	=b6

Здесь:

m₁₁ = m_лф + m_л + m_от + m_сн;

m₁₂ = m₂₁ = 0;

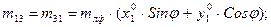
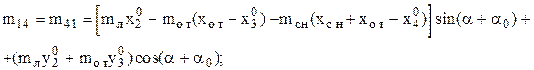
m₁₅ = m₅₁ = (m_от + m_сн)cos(a+a₀);

m₁₆ = m₆₁ = m_сн cos(a+a₀);

m₂₂ = m_лф + m_л + m_от + m_сн;

;

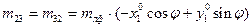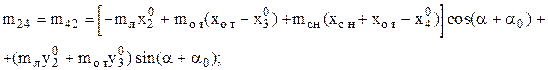
m₂₅ = m₅₂ = (m_от + m_сн)sin(a+a₀);

m₂₆ = m₆₂ = m_сн sin(a+a₀);

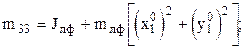
m₃₄ = m₄₃ = 0;

m₃₅ = m₅₃ = 0;

m₃₆ = m₆₃ = 0;

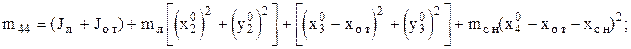
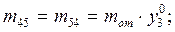
m₄₆ = m₆₄ = 0;

m₅₅ = (m_от + m_сн);

m₅₆ = m₆₅ = m_сн;

m₆₆ = m_сн;

В правой части формируются члены, содержащие обобщенные силы и первые производные.

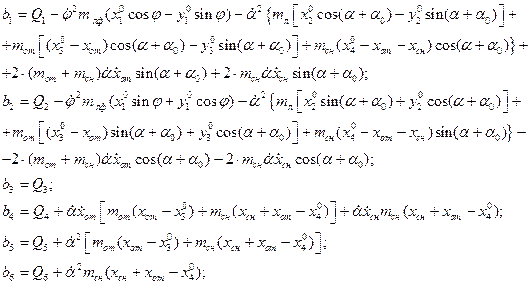
Вы видите, что даже в относительно несложной 6 степенной системе приходится оперировать с громоздкими выражениями, при выводе которых легко наделать ошибок.

Использование мощной вычислительной техники открывает большие возможности в автоматизации формирования уравнений движения.

Рассмотрим принципы таких методов.

Из рассмотренного примера видна структура уравнений

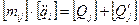
Здесь [m_ij] - некоторый тензор инерции;

[Q_j] - вектор обобщенных сил;

[Q¢_j] - вектор членов, содержащих младшие производные.

Если избавить от тензоров и векторов в этой записи и перейти к одностепенной системе, легко узнать уравнение движения точки с переменной массой (уравнение Мещерского)

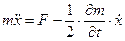
Член с переменной массой («реактивный член») связан с изменением инерционного члена при изменении положения системы. Например, в случае кулисного механизма имеем

Детальное рассмотрение уравнения Лагранжа показывает следующее:

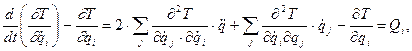
Члены тензора инерции формируются членом перед обобщенным ускорением

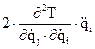
Обобщенные силы определяются инвариантностью произведенной работы от выбора системы координат при ее представлении .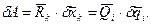

Реактивные члены представляют изменение кинетической энергии по координатам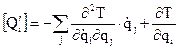

Кинетическая энергия представляется квадратичной формой в виде произведения тензоров

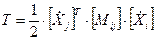, где

[M_ij] -члены тензора инерции системы

Для системы с одной степенью свободы это скаляр: масса тела М при поступательном движении, либо момент инерции J при вращении.

Для системы с тремя степенями свободы это матрица 3х3:

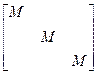для поступательных движений,

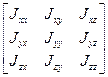для вращательного движения или комбинированные для сложных движений и числа степеней свободы более 3.

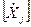- вектор скорости движения тел системы в инерциальной системе координат (НСК).

Представим этот вектор в системе обобщенных координат. Это некоторая система смещенных координат (ССК) и преобразование вектора из одной системы координат в другую подчиняется рассмотренным правилам преобразования координат и скоростей, которые мы представим в обобщенном виде:

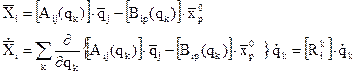
Раскроем матрицу преобразования скорости

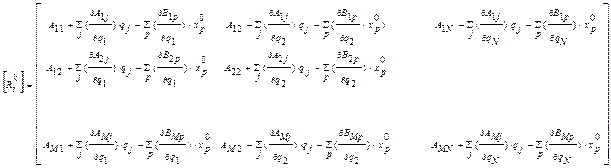
Если матрицы A_ij и B_ip не зависят от координат, то преобразование скорости производится в соответствии с матрицей A_ij преобразования перемещений.

Подставив значения преобразования скоростей в выражение для кинетической энергии имеем:

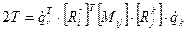
Продифференцировав это выражение, получим члены тензора инерции и вектора «реактивных» членов:

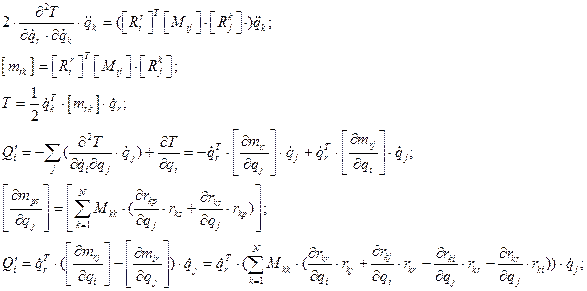
Обобщенные силы определяются выражением:

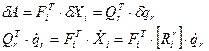
Вследствие независимости обобщенных координат имеем

.

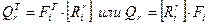В результате мы получили необходимую систему уравнений

.

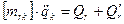Однако, метод получения компонент уравнения предельно формализован и ориентирован на автоматическое формирование программой ЭВМ.

Разработчик должен выбрать обобщенные координаты, системы координат и указать преобразования координат А_ij и B_ip.(то есть разобраться с физической моделью). Остальные преобразования осуществляются в автоматическом режиме ЭВМ.

Чтобы понять, как это осуществляется, рассмотрим ту же задачу в матричной постановке.

Физическая модель задачи и обобщенные координаты и системы координат естественно те же.

Матрицы преобразований координат выглядят следующим образом:

Матрица [A_ij ]

xoi qi	X	Y	j	a	xот	хсн
Х01
Y01
j
X02
Y02
a
X03					cos(a+a0)
Y03					sin(a+a0)
X04					cos(a+a0)	cos(a+a0)
Y04					sin(a+a0)	sin(a+a0)

Из строк матрицы [A_ij ] получаются помеченные в таблице координаты массивных тел системы в НСК. Над столбцами размещены компоненты вектора обобщенных координат, на которые перемножаются строки матрицы для выражения координат НСК.

Компоненты матрицы становятся понятны, если вернуться к рассмотренным в предшествующей постановке выражениям координат

Матрица [B_il ]

	x1^0	y1^0	j^0	x2^0	y2^0	a^0	x3^0	y3^0	x4^0
X01	cosj	-sinj
Y01	sinj	cosj
j^0
X02				cos(a+a0)	-sin(a+a0)
Y02				sin(a+a0)	cos(a+a0)
a^0
X03							cos(a+a0)	-sin(a+a0)
Y03							sin(a+a0)	cos(a+a0)
X04									cos(a+a0)
Y04									sin(a+a0)

Из строк матрицы [B_il ] получаются компоненты вектора смещения начал координат используемых местных и смещенных систем в НСК. Над столбцами размещены компоненты вектора начальных положений, заданного в удобных для подготовки исходных данных координатах, на которые перемножаются строки матрицы для выражения вектора смещения.

Вид матрицы масс исходной системы [M_rk]

	X01	Y01	j	X02	Y02	a	X03	Y03	X04	Y04
X01	mлф
Y01		mлф
j			Jлф
X02				mл
Y02					mл
a						Jл+Jот
X03							mот
Y03								mот
X04									mсн
Y04										mсн

J_лф, J_л, J_от - моменты инерции, лафета, люльки и откатных частей относительно собственных центров тяжести.

Проведя дифференцирование, получим вид матрицы преобразования скоростей

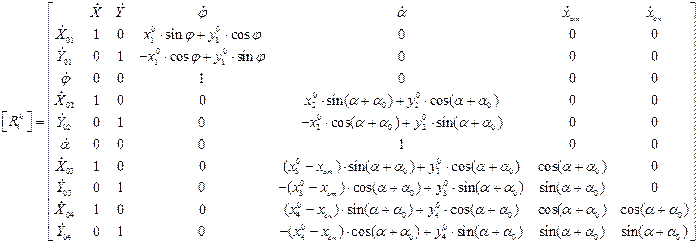
Построение матрицы матрицы масс, обобщенных сил и «реактивных» сил рекомендуется провести самостоятельно и сравнить с выражениями, полученными методами прямого дифференцирования.

В этом Вам окажут помощь методические указания к практическим занятиям по курсу лекций "Динамика импульсных тепловых машин" НГТУ. Н.Новгород. 1997г.:

В.Е. Слуцкий. Вывод уравнений движения арторудия при выстреле (плоская модель).

В.Е. Слуцкий. Вывод уравнений движения арторудия при выстреле матричным методом (плоская модель).

Дата добавления: 2014-01-14