Уравнения неразрывности движения и деформации звеньев

Для описания движения механизма как единого целого одних уравнений движения и равновесия недостаточно. Необходимо записать уравнения связи, не позволяющие системе разделиться на отдельные части.

В теории механизмов и машин вы рассматривали связь звеньев механизма между собой и с ведущим звеном через систему передаточных отношений, характеризующих соотношение малых перемещений звеньев при сдвиге одного из них:

.

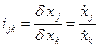Для построения этих отношений вас учили приемам построения положений механизма при движении, построения планов скоростей и методам определения передаточных отношений с их использованием. Умение их использовать очень полезно для выполнения грубых оценок и прикидок. Для более детальных расчетов, как правило, используются аналитические методы.

В курсе импульсных тепловых машин в качестве таких уравнений используются уравнения неразрывности движения и деформации звеньев. Особенностью движения динамических систем с ударными нагрузками является необходимость учета деформаций звеньев.

Рассмотрим весьма удобный аналитический способ написания уравнений связи – метод векторных контуров.

Существо метода в том, что точки звеньев системы, положение которых неизвестно в пространстве, последовательно связываются цепочкой векторов с точками, положение которых определено. Система становится геометрически определенной.

Записав компоненты этих векторов на оси координат, получим аналитические выражения, определяющие положения неизвестных точек звеньев и, соответственно, самих звеньев. Для упрощения представления этих уравнений в виде программной реализации максимально формализуем этот процесс.

Рассмотрим написание уравнений связи на примере.

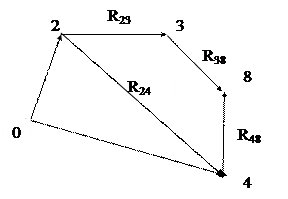
Схема механизма представлена на рисунке 10.

Механизм состоит из 6 звеньев, 1 и 6-е - массивные, 5-е - упругое. Упругое звено связывает звенья 4 и 6, которые лежат в параллельных плоскостях. Центры МСК звеньев 5 и 6 совпадают.

Известные перемещения:j₁,j₆.

Неизвестные перемещения: х₁₇, у₁₇, х₂₇, у₂₇, j₂, j₃, j₄, dj₅ - 8 неизвестных.

Рис.10. Схема механизма (координаты и деформации).

Рассмотрим построение векторных контуров.

Простейший контур, координирующий положение звеньев 2, 3 и 4, связывает расположение звеньев с известными координатами точек закрепления- разворота 2 и 4.

Спроектируем векторы на оси НСК

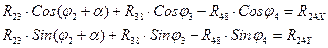
В результате получили 2 нелинейных уравнения, связывающих неизвестные координаты звеньев j₂,j₃,j_4.

Формализуем построение

Координаты вектора R₂₃ представим разностью координат (радиус-векторов) точек 2 и 3, R_{38 -}точек 3 и 8, R_{48 -}точек 4 и 8, R_{24 -}точек 2 и 4.

На первый взгляд получили тождество: раскрой скобки и получишь 0=0.

Но проведем преобразования координат и представим эти векторы в местных системах координат.

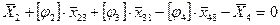
Получены 2 аналогичных нелинейных уравнения, связывающих неизвестные координаты звеньев j₂,j₃,j_4.

Однако решать нелинейные уравнения трудоемко и неудобно.

Если продифференцировать их по времени, то получим соотношения между скоростью изменения координат, но они уже будут линейными. Причем, члены, не изменяющиеся во времени, из них исчезают.

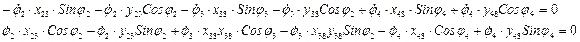Запишем уравнения, связывающие положения звеньев 1 и 2

Векторный контур

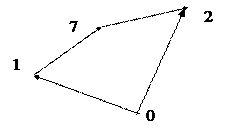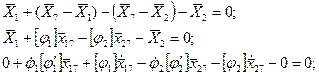
Два векторных контура сформировали 4 уравнения, а неизвестных 8.

Для формирования дополнительных уравнений рассмотрим связь углов поворота звеньев 4 и 6 в параллельных плоскостях через упругое звено 5

.

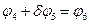
Также рассмотрим связи в точке взаимодействия копиров 7.

Для копира на звене 1

Для копира на звене 2

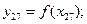
Направление нормали в точке контакта 2-х копиров

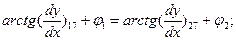
Взяв производные по времени, снова получим линейные уравнения относительно скорости изменения координат:

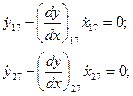
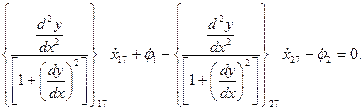
Таким образом, мы получили систему 8 линейных алгебраических уравнений относительно 8 неизвестных изменений координат.

Представим систему уравнений в табличной форме (см.табл.2)

Решение линейной системы определяет вектор изменения положения (скоростей) звеньев участка механизма.

Система уравнений неразрывности движения и деформаций Таблица 2

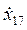
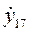
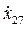
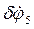
комментарий										b
контур 1	cosj1	- sinj1	- cosj2	sinj2	x27sinj2+ +y27cosj2				=	[x17sinj1+ +y17cosj1]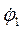
sinj1	cosj1	- sinj2	cosj2	-x27cos j2+ +y27sin j2				=	[-x17cosj1+ +y17sinj1]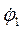
копирные связи									=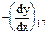
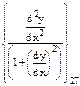
				-1				=	-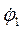
								=
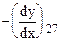
контур 2					-x23sinj2- -y23cosj2	-x38sinj3- -y38cosj3	x48sinj4+ +y48cosj4		=
				x23cosj2- -y23sinj2	x38cosj3- -y38sinj3	-x48cosj4+ +y48sinj4		=
Упругая связь									=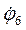

Для определения положения звеньев, координат и деформации запишем систему дифференциальных уравнений:

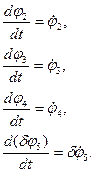
Начальные условия:

при t=0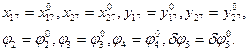

Система дифференциальных уравнений решается одним из численных методов одновременно с решением уравнений движения массивных звеньев.

Предложенный способ совершенно четко направлен на машинную реализацию.

Запишем правила построения уравнений связи:

1. На схеме механизма производится нумерация звеньев и кинематических пар в следующем порядке:

-нумеруются центры МСК звеньев, начиная с одного массивного звена к другому (или стойке),

- последовательно нумеруются другие кинематические пары.

2. С центрами МСК связываются местные системы координат звеньев.

3. Формируется состав неизвестных и известных координат уравнений связи:

к неизвестным координатам, как правило, относятся положения МСК звеньев, координаты точек контакта на копирах (высших КП), деформации упругих звеньев;

к известным координатам относятся положения точек опоры на стойке, координаты массивных звеньев (они определяются уравнениями движения).

4. Для построения уравнений связи подбирается система “независимых” векторных контуров, соединяющих через кинематические пары центры МСК малоинерционных звеньев с МСК массивных звеньев или точками стойки.

`х<sub>01</sub> + (`х₂ - `х<sub>1</sub>) +¼+ `х_ON =0.

Каждый контур представляет собой замкнутый векторный многоугольник, составляемый из векторов (`х<sub>k</sub> - `х_i), соединяющих КП и центр МСК звена. Вектор имеет знак +, если направление обхода «центр МСК – КП» совпадает с направлением обхода векторного многоугольника.

Контур начинается и заканчивается составляющей `Х<sub>0</sub> в центре МСК массивного звена или точке стойки. Вектор `Х₀ соединяет эту точку с центром НСК.

Контур, который можно получить наложением нескольких выбранных ранее контуров, является “зависимым” и не включается в систему уравнений.

Каждый векторный многоугольник формирует (в плоскости) два уравнения связи, являющиеся проекциями векторного равенства на оси НСК.

5. В случае, если упругое звено соединяет звенья в параллельных плоскостях, угловая связь между ними формирует дополнительное уравнение

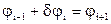, деформация звена помечается знаком d.

6. Координаты точки контакта на кинематических парах типа копир определяются дополнительными уравнениями, которые отражают форму копира и взаимодействие в точке контакта по единой нормали.

Для копира на звене i:

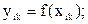
Для копира на звене i+1: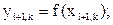

Направление нормали в точке контакта 2-х копиров

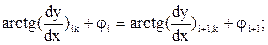
7. Суммарное количество уравнений должно быть достаточным для определения неизвестных.

8. Для того, чтобы сделать систему уравнений связи линейной, формируем ее относительно вариации перемещений системы или просто скоростей перемещения.

8.1 При этом начальный и конечный вектор векторного многоугольника преобразуется следующим образом:

если координаты заданы в НСК `;

если координаты заданы в смещенной системе координат ССК,

,

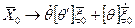где q - угловой разворот ССК относительно НСК;

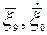- вектор координаты и скорости точки 0 в ССК;

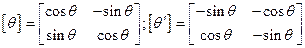-матрица углового преобразования ССК в НСК и ее производная.

8.2 Промежуточный вектор преобразуется следующим образом:

,

где - координаты и скорость точки k в МСК звена i;

- угловой разворот МСК относительно НСК и угловая скорость;

[j],[j¢] - матрица углового преобразования МСК в НСК и ее производная.

8.3 Уравнение связи через упругое звено углов поворота звеньев в параллельных плоскостях:

,

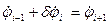8.4 Уравнения контакта на копире:

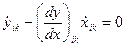(уравнение касательной);

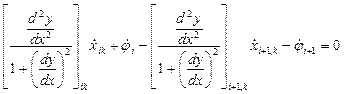- (уравнение нормали).

8.5 Известные компоненты переносятся в правую часть уравнения.

9. Линейная система уравнений решается относительно неизвестных составляющих, представляющих скорости изменения координат.

10. Для определения неизвестных координат (перемещений) дополнительно решается система дифференциальных уравнений вида

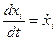, при начальных условиях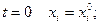

Построенная таким образом система требует от разработчика указания последовательности связываемых точек, типа точки и типа связи (линейный, угловой контуры или взаимодействие копиров). После этого уравнения связи могут быть построены системой автоматически.

Дата добавления: 2014-01-14