Свойства ЭФМ

Как отмечалось в начале курса при описании физической модели механической системы, элемент физической модели (ЭФМ) представляет собой «упругий колебательный контур», включающий в свой состав массивные, упругие и малоинерционные звенья. Он возбуждается и совершает свои колебания под действием внешнего возбуждающего воздействия на окаймляющие ЭФМ массивные звенья в виде силового или кинематического возмущения произвольной формы.

Возбуждающая нагрузка всегда может быть представлена либо в виде импульса действующей силы при кратковременном воздействии, либо суммой гармоник при длительном воздействии. Любое воздействие, осуществляемое по закону произвольной формы, может быть представлено разложением в ряд Фурье суммарным воздействием нагрузок, изменяющихся по гармоническому закону с различной амплитудой и частотой.

Чтобы понять физику происходящих в ЭФМ явлений рассмотрим их на примере простейшего ЭФМ сначала отдельно, а затем во взаимодействии с другими ЭФМ.

Простейшее ЭФМ может быть представлено в виде взаимодействия двух масс через пружину:

Система уравнений, описывающая движение звеньев ЭФМ, запишется следующим образом:

Два массивных тела совершают колебательное смещение относительно друг друга .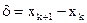

Уравнение колебаний запишется:

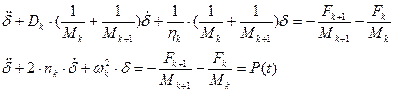
где

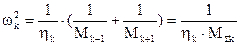- круговая частота собственных колебаний подсистемы;

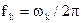- собственная частота колебаний подсистемы;

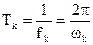- период собственных колебаний подсистемы;

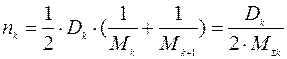- коэффициент вязкого сопротивления;

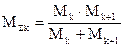- приведенная масса ЭФМ;

P(t) – внешняя нагрузка.

Без воздействия внешней силы при наличии начального неравновесного смещения или скорости смещения тел (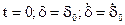) система осуществляет свободные колебания, подчиняясь следующему закону:

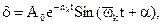где:

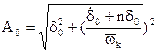- амплитуда собственных колебаний;

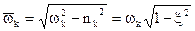- круговая частота затухающих колебаний;

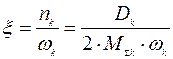- относительный коэффициент демпфирования;

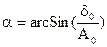- начальная фаза колебаний.

Если внешняя нагрузка представляется гармоническим возмущением вида: то решение примет следующий вид:

.

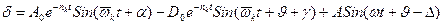Первое слагаемое описывает свободные колебания системы.

Третье слагаемое отображает вынужденные колебания. При этом амплитуда колебаний равна 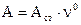, а сдвиг фазы перемещения относительно фазы возмущающей силы 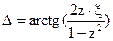, где:

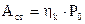- статическая амплитуда, т.е. отклонение системы под действием силы Р₀, приложенной статически;

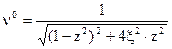- коэффициент динамичности;

- отношение частот вынужденных и собственных колебаний.

Второе слагаемое определяет сопровождающие колебания, частота которых равна частоте собственных колебаний w_к, а амплитуда и фаза – от амплитуды и фазы вынужденных колебаний и определяются по формулам:

- амплитуда сопровождающих колебаний;

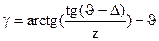- сдвиг фазы сопровождающих колебаний.

Свободные и сопровождающие колебания играют существенную роль в начале движения, при переходных процессах, а затем их амплитуда убывает по экспоненте. В установившемся процессе (t®¥) участвуют лишь вынужденные колебания.

В случае, если частота вынужденных колебаний совпадает с частотой собственных колебаний (z=1) наступает явление резонанса. При этом амплитуда колебаний системы быстро нарастает. Происходит накопление энергии. Поскольку возрастание амплитуды происходит только сопровождающих и вынужденных колебаний, для большей наглядности результата рассмотрим случай, когда для нулевых начальных условий А₀=0. Имея в виду, что при резонансе сдвиг фазы колебаний отстает от фазы возмущающей силы на p/2, выражение для величины смещения при резонансе примет вид:

.

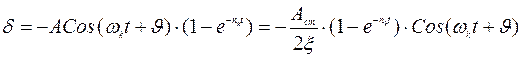Таким образом, если при t=0 имеем d=0, то при t®¥ dmax = Acт/2x.

При малом демпфировании n_k® 0 решение дифференциального уравнения принимает вид 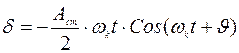и амплитуда вынужденных колебаний возрастает бесконечно.

Изменение амплитуды колебаний (коэффициента динамичности) в зависимости от отношения частот и относительного демпфирования представлено на рис. 15.

Рис.15 Изменение коэффициента динамичности в зависимости от отношения частот и относительного демпфирования

x=0,01; x=0,1; x=0,2; x=0,4; x=0,6;

Большой практический интерес представляет изменение максимального значения амплитуды при прохождении резонанса. Такая ситуация нередко возникает при разгоне и остановке машин, если частота собственных колебаний отдельных подсистем находится ниже частоты установившихся колебаний, задаваемых внешним возмущением. Это могут быть возмущения, вызванные работой двигателя САО, или вращением гребного винта корабля. На рис.16 представлено изменение коэффициента динамичности в зависимости от скорости увеличения возбуждающей частоты.

Рис.16. Изменение коэффициента динамичности в зависимости от параметра скорости изменения возбуждающей частоты.

Здесь:

n*/n⁰ – отношение максимального коэффициента динамичности возникающего при изменении возбуждающей частоты к максимальному коэффициенту динамичности при резонансе в установившемся режиме;

- параметр скорости изменения частоты.

При высокой скорости разгона и торможения резонанс не успевает развиться. Если же значения параметра скорости изменения частоты h>1, то резонанс успевает развиться в полной мере, и необходимы специальные мероприятия по борьбе с этим явлением.

Если действующая на систему сила представляет сумму двух гармоник 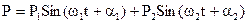, причем частоты w₁ и w₂ отличаются незначительно, то возникают биения, показанные на рис.17.

Рис.17 График биений при возмущающих колебаниях с близкими частотами.

Частота колебаний ;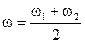

Период колебаний ;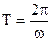

Период биений ;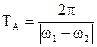

Максимальная амплитуда колебаний ;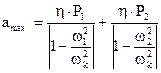

Минимальная амплитуда колебаний .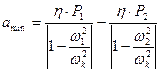

Если на систему действует произвольная возмущающая сила, то решение может быть представлено следующей формулой, описывающей и свободные, и сопровождающие и вынужденные колебания (при x<1):

.

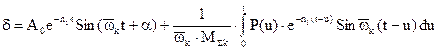Если длительность действия возмущающей силы очень мала по сравнению с периодом собственных колебаний (t*<<T_k), то колебания в невозмущенной системе могут быть оценены по импульсу воздействующей силы ():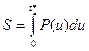

.

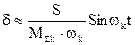Чтобы понять физику взаимодействия нескольких ЭФМ сначала рассмотрим общий подход к решению задач в многомассовых колебательных системах. При рассмотрении этого вопроса ограничимся случаем свободных колебаний без учета явлений диссипации. Описывающая система дифференциальных уравнений при этом имеет вид:

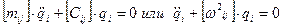, (а) при начальных условиях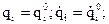

где:

[m_ij] – тензор инерции системы;

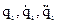- векторы перемещения, скорости и ускорения масс системы;

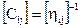- тензоры жесткости и податливости системы;

- матрица квадратов круговых парциальных частот подсистем общей динамической системы.

Решения этой системы будут следующие зависимости, определяющие свободные колебания системы:

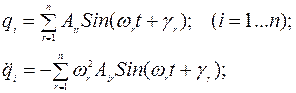(б)

Таким образом, каждая масса участвует в сложном колебательном движении, представляющем собой сумму главных колебаний, каждое из которых имеет одну из собственных частот w_r.

Для определения собственных частот решается уравнение частот системы. Оно записывается из условия, что определитель системы линейных уравнений для нахождения амплитуд колебаний A_ir(для этого решения (б) подставляются в уравнения (а)) должен быть равен 0, чтобы решения не были нулевыми.

Это уравнение имеет n корней и при колебаниях около положения устойчивого равновесия все эти корни вещественны и положительны. Эти n -корней представляют n -круговых частот собственных колебаний системы. Они отражают основные свойства системы и не изменяются при различных способах разбиения системы на подсистемы в отличие от парциальных частот, меняющих свои значения при этом.

Но для определения всех параметров решений надо найти еще n² значений A_ir и n значений g_r. Если вычесть 2 n связей, представляемых начальными условиями, необходимо выявить еще (n²- n) дополнительных связей между амплитудами главных колебаний, не зависящих от начальных условий. Роль последних выполняют коэффициенты формы(коэффициенты распределения)a_ir, устанавливающие соотношения между амплитудами А_ir при фиксированной собственной частоте w_r: 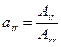. Они определяются из уравнений (а) подстановкой в них решений (б), выраженных через собственные формы.

. Учитывая, что a_rr=1, получим (n²- n) невырожденных уравнений для определения коэффициентов формы главных колебаний с частотами w_r.

Далее мы рассмотрим взаимодействие двух простейших ЭФМ, представленных на рис.18.

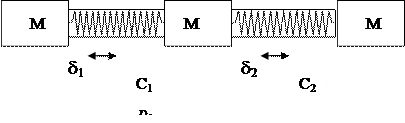Рис.18 Схема взаимодействия простейших ЭФМ.

Уравнения колебаний, приведенные к относительным перемещениям, имеют вид:

или, выраженные через парциальные частоты:

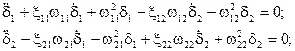
Уравнение частот запишется в виде:

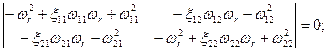
В развернутом виде это полное уравнение 4 степени, не имеющее аналитического решения:

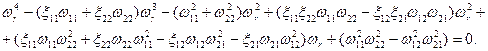
Здесь: 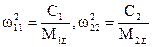- парциальные частоты ЭФМ1 и ЭФМ2;

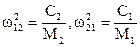- парциальные частоты связи ЭФМ;

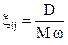-коэффициенты относительного демпфирования.

Для случая малых коэффициентов относительного демпфирования обе собственные частоты определяются из биквадратного уравнения:

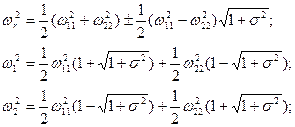
Собственные формы соответствующие круговым собственным частотам главных колебаний w₁ и w₂ определяются по следующим формулам:

Форма для колебания с частотой w₁:

;

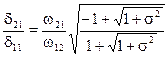Форма для колебания с частотой w₂ симметрична:

.

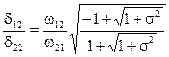Здесь 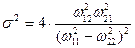- коэффициент связности подсистем.

На рис.19 и 20 показано соотношение парциальных частот ЭФМ и собственных частот механизма, а также соотношение форм колебаний в зависимости от связности ЭФМ и соотношения их парциальных частот.

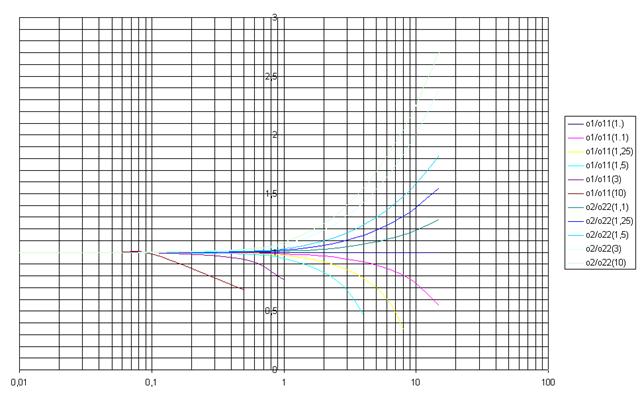
Рис.19 Сравнение собственных частот системы и парциальных частот ЭФМ при различной связности и соотношении парциальных частот.

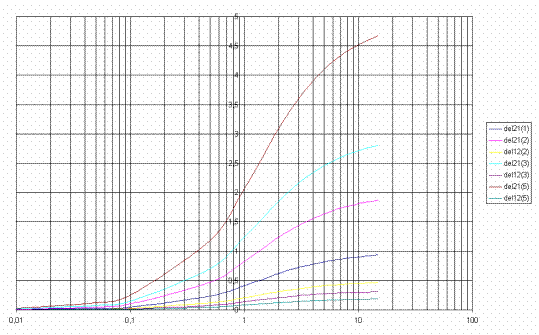
Рис.20 Соотношения коэффициентов формы при различной связности и отношениях частот связи.

Графики наглядно показывают:

Чем больше связность, тем больше взаимное влияние ЭФМ. При малой связности процессы, происходящие в ЭФМ, практически независимы, и их можно рассматривать практически раздельно. Две частоты собственных колебаний полной системы при этом мало отличаются от парциальных частот ЭФМ.

Аналогично ведут себя и формы колебаний. Они также определяются в основном коэффициентом s. При малом s на каждой собственной частоте наблюдаются колебания только в одной ЭФМ, а в другой они практически не возбуждаются.

Представленные графики наглядно иллюстрируют физическую сущность элементов физической модели. Однако, рассматривая их, не надо упускать из виду, что в целом построенная в курсе математическая модель описывает и решает задачи с использованием разнообразных ЭФМ, систем любой связности без какой-либо потери точности вычислений.

Дата добавления: 2014-01-14