Деление механической системы на ЭФМ

Задача разделения расчетной модели на элементы физической модели является одной из важнейших задач рационального построения решения, которое правильно описывает исследуемые явления, удовлетворяет необходимой точности результатов и требует для реализации минимального времени.

Разделение механической системы на ЭФМ заключается в правильной оценке вклада различных звеньев в колебательный процесс, выделении массивных, упругих и малоинерционных звеньев.

Казалось, существует простейшее решение – все звенья принять массивными, а между ними поместить условные упругие звенья, отражающие свойства деформируемости, диссипации и зазора. Однако этот подход не является рациональным. Численная модель будет реализовывать весь спектр колебаний: и значительные, определяющие функционирование механизма, и мелкую дрожь в звеньях системы, определяющую не движение, а шумовой эффект. Если исследование дрожи не является целью расчета, то строить такую модель нецелесообразно. Высокочастотные колебания для своего корректного отражения требуют очень малого шага интегрирования, на который автоматически настроится система интегрирования, а это повлечет существенное (в десятки раз) удлинение времени решения динамической задачи. А время решения серьезной динамической задачи нередко достаточно велико.

Для разработки правильного подхода к делению расчетной модели на ЭФМ рассмотрим поведение двух простейших парциальных систем и преобразование ими гармонического возмущения A*Sin wt.

Для парциальной подсистемы 1 типа имеем:

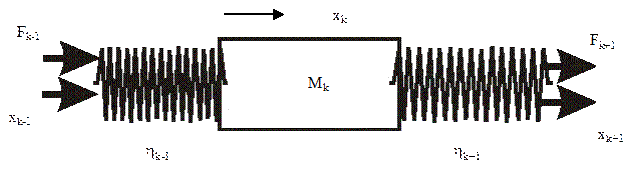
Система уравнений, описывающая парциальную подсистему:

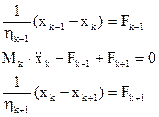
или для колеблющейся массы

,

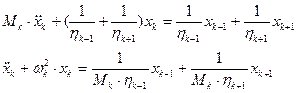где

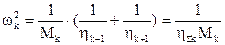(а) - собственная частота колебаний подсистемы;

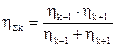- приведенная податливость подсистемы.

При воздействии гармонического возмущения, исключив переменные с индексом к, выразим возмущения, получаемые концом (к+1), от воздействия возмущения на конце (к-1) [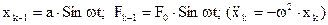]. При этом имеем:

перемещение конца пружины на выходе из подсистемы после прохождения через нее гармонического возмущения поданного на вход: ;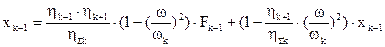

усилие на конце пружины на выходе из подсистемы после прохождения через нее гармонического возмущения поданного на вход: .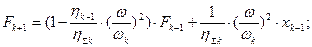

В самой парциальной подсистеме, если она не перемещалась, возникают сопровождающие с частотой w_к и вынужденные колебания с частотой w.

При 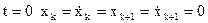имеем

.

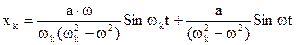Для парциальной подсистемы 2 типа имеем:

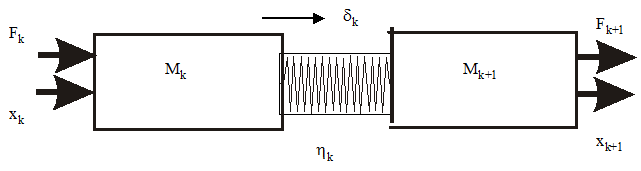
Система уравнений, описывающая парциальную подсистему:

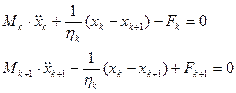
Два массивных тела совершают колебательное смещение относительно друг друга 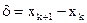. Уравнение колебаний запишется:

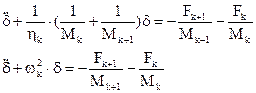
где

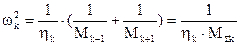(б) - собственная частота колебаний подсистемы;

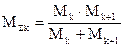- приведенная масса подсистемы.

Выразив возмущения массы М_к+1 на конце (к+1) через возмущения, воздействующие на массу М_к, для случая гармонического возмущения 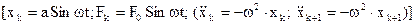имеем:

перемещение массы М_к+1 на выходе после прохождения через подсистему гармонического возмущения поданного на вход:

;

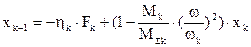усилие на выходе из подсистемы после прохождения через нее гармонического возмущения поданного на вход:

.

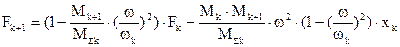В самой парциальной подсистеме, если она не перемещалась, возникают сопровождающие с частотой w_к и вынужденные колебания с частотой w.

При 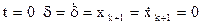имеем:

.

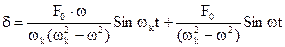Рассмотрим возбуждение механизма от действия импульсной нагрузки. Это типично для артиллерийских систем при производстве выстрела. Представим схематически механизм (см. рис. 21) и формирование колебания в нем под действием импульсной нагрузки приложенной к одному из тел механизма.

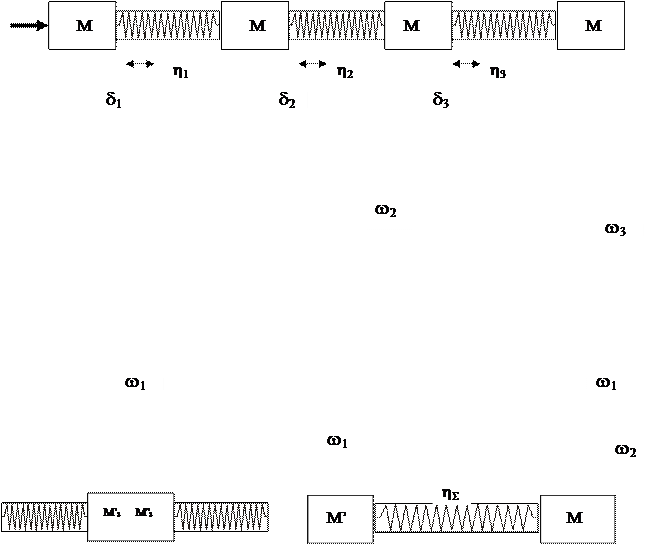
Рис.21. Схема формирования колебательного движения под действием импульсной нагрузки, поясняющая принцип уменьшения числа степеней свободы механизма.

Импульсная нагрузка, воздействуя на тело 1, возбуждает собственные колебания в подсистеме 1 с собственной круговой частотой w₁, которая возбуждает тело 2 и собственные, сопровождающие (с собственной круговой частотой w₂) и вынужденные (с круговой частотой w₁) колебания в подсистеме 2. Складываясь, они формируют колебания подсистемы 2.

Далее эти две гармоники возбуждают колебания в подсистеме 3 (собственные, сопровождающие с собственной круговой частотой w₃ и вынужденные с круговыми частотами w₁ и w₂ )

Если резонансные явления отсутствуют, то по цепочке звеньев передается один и то же энергетический импульс и, соответственно, амплитуды последовательно возникающих колебаний будут обратно пропорциональны возбуждающим их частотам (с учетом рассеивания энергии и разделения по гармоникам). Это следует из следующего рассуждения о передаче кинетической энергии по подсистемам:

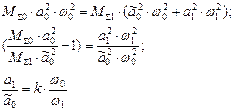
Если частоты собственных и вынужденных колебаний близки, то суммарные колебания в подсистеме определяются колебаниями обоих частот. Если же частоты существенно различаются, то высокочастотная составляющая оказывает незначительное воздействие на суммарные колебания. Ее амплитуда меньше и она быстро затухает.

В этом случае воздействием высокочастотного вынуждающего колебания можно пренебречь без ущерба для точности расчета. Это производится преобразованием парциальной подсистемы одно типа в другой. Чтобы не исказить характеристик механизма, масса и упругие свойства преобразуемой подсистемы не удаляются, разделяются по элементам принимающей подсистемы таким образом, чтобы сохранились частотные свойства и, соответственно, энергетика преобразуемой подсистемы.

Если заменить подсистему 1типа подсистемой 2 типа, параметры которой равны:

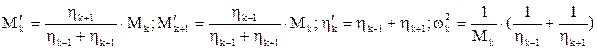(в)

то собственная частота преобразуемых подсистем сохранится (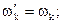), а выражения для передаваемого гармонического возмущения примут вид:

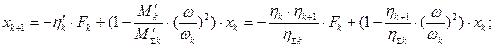
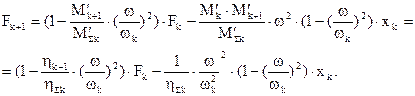
Если заменить подсистему 2типа подсистемой 1 типа, параметры которой равны:

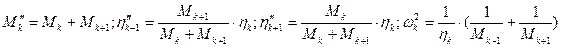(г)

то собственная частота преобразуемых подсистем сохранится (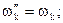), а выражения для передаваемого гармонического возмущения примут вид:

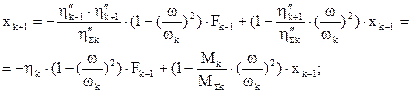
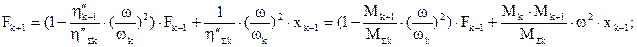
Как видно из преобразований, возмущение, поглощаемое подсистемой и передаваемое по цепочке другим звеньям, пропорционально отношению возбуждающей подсистему частоты и собственной частоты подсистемы 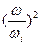. Более того, величина передаваемого возмущения при замене подсистемы одного типа подсистемой другого типа практически совпадает, отличаясь в отдельных членах на множитель 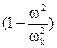. Так что основная и заменяющая система, в случаях когда 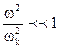, эквивалентны, и соответствующее уменьшение числа степеней свободы не вносит погрешностей в динамический расчет. Более детальными и точными исследованиями Л.Я.Банаха показано, что погрешности в собственных формах упрощенной системы не превышают 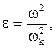а в собственных частотах e².

Как было показано, в случаях импульсных возмущений системы, возбуждающими колебаниями являются колебания соседних подсистем с возбуждающей частотой ее собственных колебаний w_к. Соответственно, .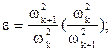

В случаях воздействия внешней вибрационной нагрузки (в транспортной динамике, в динамике работы орудия в условиях колеблющегося моря), возбуждающим колебанием является внешнее возмущение с его частотой w. Соответственно, .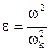

В качестве меры определяющей возможность преобразования обычно принимают величину отношения e = 10%, что примерно соответствует точности динамического расчета.

В случае, если <0,1, высокочастотная подсистема преобразуется в подсистему другого типа, уменьшая число степеней свободы системы. Этот процесс преобразования продолжается до тех пор, пока во всех подсистемах отношение e не станет более 10%.

Рассмотрим практический пример рационального разделения механической системы на ЭФМ.

Любая механическая система может быть упрощенно представлена несложным преобразованием совокупностью масс и пружинок, приведенных к одному энергетическому уровню. Эти приемы изучались Вами в теоретической механике и теории механизмов и машин. Причем, при разделении на ЭФМ для оценки приведенных масс и приведенных податливостей не требуется точных расчетов. На точность дальнейших расчетов эта предварительная работа влияет очень слабо.

На рис. 22в строке 3представлен пример такой системы. Разобьем ее на парциальные подсистемы 1 и 2-го типа № этих подсистем указаны в строках 1 и 2. Характеристики инерции и упругости звеньев системы указаны в строках 4 и 5.

Подсчитаем по вышеприведенным формулам (а) и (б) квадраты собственных частот подсистем 1 и 2-го типа и сравним значения частот соседних гармоник. Квадраты собственных частот для подсистем 1 и 2 типа приведены в строках 6 и 7. В выделенных цветом ячейках указаны соотношения квадратов частот соседних гармоник(1/e). Для подсистем 1 типа 1/e>10 для первой и второй и пятой и шестой подсистем. Во всех остальных случаях и для всех подсистем 2-го типа 1/e<10. В соответствии с вышеотмеченным порядком преобразуем более высокочастотные гармоники 1-го типа 2 и 5 в гармоники 2-го типа. Инерционные характеристики и податливости звеньев при этом пересчитываются по формулам (в). Вид системы 1 ступени упрощения представлен в строке 8, а уточненные характеристики массы и податливости в строках 9 и 10. Снова подсчитаем квадраты собственных частот для подсистем 1 и 2 типа. Они приведены в строках 11 и 12. В выделенных цветом ячейках указаны соотношения квадратов частот соседних гармоник(1/e). У подсистем 1-го типа 1/e>10 для 1-ой и 3-ей подсистем, для всех остальных подсистем и подсистем 2-го типа 1/e<10.

Снова преобразуем более высокочастотную подсистему 3 к типу 2, выполнив следующую ступень упрощения. Вид системы 2 ступени упрощения представлен в строке 13, а уточненные характеристики массы и податливости в строках 14 и 15. Снова подсчитаем квадраты собственных частот для подсистем 1 и 2 типа. Они приведены в строках 16 и 17. В выделенных цветом ячейках указаны соотношения квадратов частот соседних гармоник(1/e). Для всех ост подсистем 1-го и 2-го типа 1/e<10.

На этом упрощение системы заканчивается. В качестве массивных звеньев принимаются звенья 1, 4, 6 и 7. Звенья 2, 3 и 5 следует принять малоинерционными. Первое ЭФМ включает массивные звенья 1 и 4, а также малоинерционные 2 и 3. Второе ЭФМ включает массивные звенья 4 и 6, а также малоинерционное 5. Третье ЭФМ включает массивные звенья 6 и 7, а четвертое ЭФМ - массивные звенья 7 и 8. Эти ЭФМ малоинерционных звеньев не имеют.

Таким образом, формируется оптимальная физическая модель механической системы и в соответствии с ней строится математическая модель, осуществляется ее решение, анализ результатов и их использование в практической деятельности при проектировании артиллерийских установок.

№ подсистемы 1 типа
№ подсистемы 2 типа
Исход. схема механизма
Масса, М, кг			7,5		6,5				3,6		8,8		8,4
Податливость, h, м/Н		0,13		0,19		0,05		0,039		0,28		0,30		0,039
Собст. частота подсистемы 1 типа, w^2 (1)	0,0496	34,8	1,727	2,2	3,88	2,04	1,90	4,3	8,11	10,3	0,78	4,3	3,4	2,2	1,51
Собст. частота подсистемы 2 типа, w^2 (2)		1,075	1,4	1,511	2,6	3,91	2,1	8,19	5,8	1,398	1,8	0,776	5,9	4,56
1 ступень упрощения
М	159,7		9,7		27,2		9,2		8,4
h		0,32		0,05		0,319		0,30		0,039
w^2 (1)	0,0196	121,6	2,38	2,8	0,85	1,2	0,73	4,6	3,4	2,2	1,51
w^2 (2)		0,342	8,2	2,79	6,1	0,456	1,7	0,759	6,0	4,56
2 ступень упрощения
М			35,5		9,2		8,4
h		0,37		0,319		0,30		0,039
w^2 (1)	0,0168	9,8	0,164	4,4	0,73	4,6	3,4	2,2	1,51
w^2 (2)		0,093	4,6	0,429	1,8	0,759	6,0	4,56

Рис.22 Упрощение механической системы с целью выделения массивных звеньев и разделения на ЭФМ.

Дата добавления: 2014-01-14