Аппроксимация характеристик нелинейных элементов

Иллюстрация указанного воздействия на реальный полупроводниковый диод

Как правило, ВАХ нелинейных элементовi = F(u) получают экспериментально, поэтому чаще всего они заданы в виде таблиц или графиков. Чтобы иметь дело с аналитическими выражениями, приходится прибегать к аппроксимации.

Обозначимзаданную таблично или графически ВАХ нелинейного элементаi = F_V(u), а аналитическую функцию, а ппроксимирующую заданную характеристику, i = F(u, a₀, a₁, a₂, …, a_N). где a₀, a₁, …, a_N — коэффициенты этой функции, которые нужно найти в результате аппроксимации.

А) В методе Чебышева коэффициенты a ₀, a ₁, …, a _N функции F(u) находятся из условия:

, (5)

т. е. они определяются в процессе минимизации максимального уклонения аналитической функции от заданной. Здесь u_k, k = 1, 2,..., G — выбранные значения напряжения u.

При среднеквадратичном приближении коэффициенты a ₀, a ₁, …, a _N должны быть такими, чтобы минимизировать величину

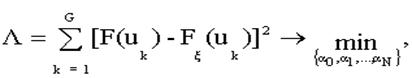(6)

Б) Приближение функции по Тейлору основано на представлении функции i = F(u)рядом Тейлора в окрестности точкиu = U₀:

(7)

и определении коэффициентов этого разложения. Если ограничиться первыми двумя членами разложения в ряд Тейлора, то речь пойдет о замене сложной нелинейной зависимости F(u) более простой линейной зависимостью. Такая замена называемся линеаризацией характеристик.

Первый член разложения F(U₀) = I₀ представляет собой постоянный ток в рабочей точке при u = U₀, а второй ч лен

- (8)

дифференциальную крутизну вольт-амперной характеристики в рабочей точке, т. е. при u = U₀.

В) Наиболее распространенным способом приближения заданной функции является интерполяция (метод выбранных точек), при которой к оэффициенты a ₀, a ₁, …, a _N аппроксимирующей функции F(u) находятся из равенства этой функции и заданной F_x(u)в выбранных точках (узлах интерполяции) u_k = 1, 2,..., N+1.

Д) Степенная (полиномиальная) аппроксимация. Такое название получила аппроксимация ВАХ степенными полиномами:

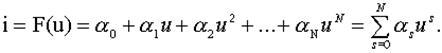(9)

Иногда бывает удобно решать задачу аппроксимации заданной характеристики в окрестности точкиU₀, называемой рабочей. Тогда используют степенной полином

(10)

Степенная аппроксимация широко используется при анализе работы нелинейных устройств, на которые подаются относительно малые внешние воздействия, поэтому требуется достаточно точное воспроизведение нелинейности характеристики в окрестности рабочей точки.

Е) Кусочно-линейная аппроксимация. В тех случаях, когда на нелинейный элемент воздействуют напряжения с большими амплитудами, можно допустить более приближенную замену характеристики нелинейного элемента и использовать более простые аппроксимирующие функции. Наиболее часто при анализе работы нелинейного элемента в таком режиме реальная характеристика заменяется отрезками прямых линий с различными наклонами.

С математической точки зрения это означает, что на каждом заменяемом участке характеристики используются степенные полиномы первой степени (N = 1) с различными значениями коэффициентов a ₀, a ₁, …, a _N.

Таким образом, задача аппроксимации ВАХ нелинейных элементов заключается в выборе вида аппроксимирующей функции и определении ее коэффициентов одним из указанных выше методов.

Воздействие гармонического сигнала на цепь с нелинейным элементом

Дата добавления: 2014-01-14