Логарифмические уравнения

Общая схема решения.

1. В искомом уравнении определяется область допустимых значений параметров, область определения задаётся некоторой системой неравенств.
2. На области определения исходное уравнение приводится к виду 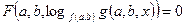. Для вспомогательной переменной 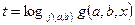это уравнение равносильно уравнению .
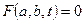3. Осуществляется решение уравнения 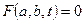на множестве допустимых значений параметров исходного уравнения. Для каждого из общих решений 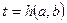уравнения определяется область 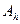значений параметров.
4. Для каждого из общих решений 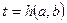на множестве 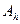проводится решение уравнения .
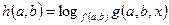5. Для общих решений 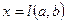этого уравнения в множестве 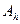устанавливается подмножество 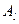значений параметров, для которых 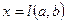является решением уравнения 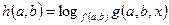и содержится в области определения исходного уравнения.
6. Всевозможные пересечения множеств 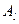для всех общих решений 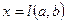определяют все типы частных уравнений.

Дата добавления: 2014-01-14