
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логарифмические неравенства
|
|
|
|
Общая схема решения.
1. Логарифмические неравенства с параметрами 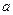 ,
, 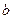 , и переменной
, и переменной 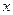 определены на множестве всех упорядоченных значений
определены на множестве всех упорядоченных значений 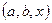 , для которых основания
, для которых основания  ,
, 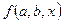 логарифмических выражений положительны и отличны от единицы, выражения
логарифмических выражений положительны и отличны от единицы, выражения 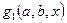 ,…,
,…,  под знаком логарифмов положительны. Исходя из этого область определения логарифмического неравенства определяется из системы
под знаком логарифмов положительны. Исходя из этого область определения логарифмического неравенства определяется из системы

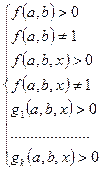 . (1)
. (1)
Определяется разбиение области определения на подмножества 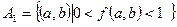 и
и  .
.
2. На области допустимых значений параметров исходное неравенство методом равносильных преобразований приводится к одному из следующих видов
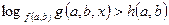 (2)
(2)
 (3)
(3)
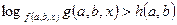 (4)
(4)
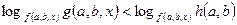 (5).
(5).
3. На области допустимых значений параметров определяются граничные значения параметров системы (1). Для найденных граничных значений в исходном логарифмическом неравенстве соответствующие частные неравенства решаются отдельно. Устанавливаются нули и точки разрыва  каждой из функций
каждой из функций 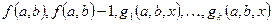 системы (1).
системы (1).
4. На области допустимых значений параметров исходного неравенства определяются граничные значения параметров уравнений


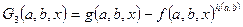 .
.
Для найденных граничных значений в исходном логарифмическом неравенстве соответствующие частные неравенства решаются отдельно.
Устанавливаются нули и точки разрыва  каждой из функций
каждой из функций 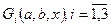 для соответствующих неравенств вида (2)-(5).
для соответствующих неравенств вида (2)-(5).
5. На каждом из множеств  и
и отдельно выделяют подмножества значений размещений, перестановок совокупности
отдельно выделяют подмножества значений размещений, перестановок совокупности 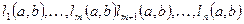 нулей и точек разрыва функций системы (1) неравенств (2)-(5).
нулей и точек разрыва функций системы (1) неравенств (2)-(5).
На множестве значений определённого размещения или перестановки методом интервалов устанавливается общее решение системы (1) и соответствующего неравенства  или общее решение системы (1) и одной из систем совокупностей
или общее решение системы (1) и одной из систем совокупностей
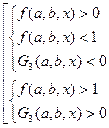
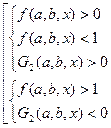 .
.
Выделенные промежутки являются общим решением некоторого неравенства на данном множестве значений параметров.
6. Множества значений параметров с одинаковыми общими решениями определяют типы частных неравенств с соответствующими характеристиками.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 401; Нарушение авторских прав?; Мы поможем в написании вашей работы!