Й случай

Приложим к балке сначала только бесконечно малую силу dΦ. Под действием этой силы система деформируется и получит какое-то перемещение dϕ, при этом сила dΦ совершит на этом перемещении работу [см. (17.1)]

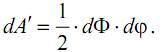
Потенциальная энергия деформации системы в этом случае

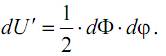
Теперь загрузим балку основной системой сил F, Φ, Ψ. Потенциальная энергия деформации балки под действием этой системы по-прежнему будет равна U (см. 1-й случай). При этом балка получит некоторое перемещение ∆.

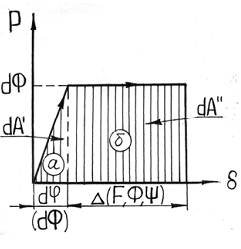
Здесь необходимо учесть, что в этот момент си-ла dΦ совершит дополнительную работу dA' на перемещении ∆ (участок б на рисунке). Так как ∆ не зависит от dΦ, то работу dA' силы в этом случае будем вычислять не по выражению (17.1), а следующим образом:

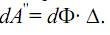
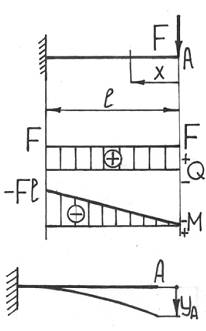
Таким образом, полную энергию деформации системы в этом случае можно вычислить так:

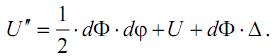
Очевидно, что энергия системы не должна зависеть от порядка приложения сил, а значит U′=U″. Тогда имеем право записать

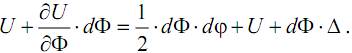
Исключая из этой формулы подобные слагаемые и пренебрегая бесконечно малыми высоких порядков, окончательно запишем

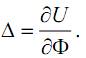
Данное соотношение есть ничто иное, как математическая запись теоремы Кастильяно, которая гласит следующее: частная производная от потенциальной энергии по обобщенной силе есть обобщенное перемещение, соответствующее этой силе.

Рассмотрим пример использования теоремы Кастильяно для определения деформаций упругой системы. Итак, для определения перемещения нам необходимо взять производную от потенциальной энергии деформации по обобщенной силе:

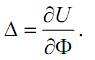
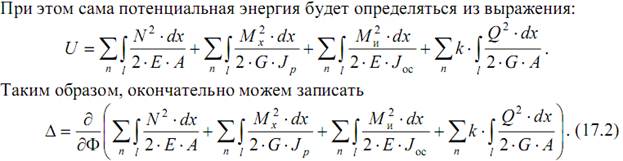
Пусть необходимо найти прогиб консольной балки под действием силы F. В этом случае в поперечных сечениях балки из шести внутренних усилий будут действовать только два – изгибающий момент Mи= –F·x и поперечная сила Q=F. Отметим, что при определении деформаций при изгибе действием поперечной силы, как правило, пренебрегают. Тогда, формулу (17.2) можем преобразовать так

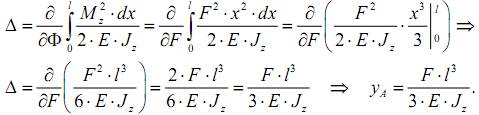
Здесь знак «плюс» показывает, что направление перемещения совпадает с направлением действия силы.

17.4. Метод нулевой фиктивной силы

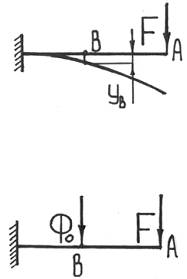Недостатком метода Кастильяно является возможность определения перемещения только в тех точках, где приложена сила и только в направлении этой силы. Если в предыдущей задаче необходимо определить перемещение точки B, то напрямую использовать теорему Кастильяно нельзя – в точке B не действует никакая сила. Тогда поступим следующим образом.

Приложим в той точке, где нужно определить перемещение, обобщенную фиктивную силу Φ0 (фиктивную, – так как ее на самом деле нет, а мы ее приложим). Вычислим потенциальную энергию деформации системы с учетом этой силы, а затем, в соответствии с (17.2), возьмем производную от энергии по этой фиктивной силе и получим формулу для определения перемещения. Для восстановления действительных условий нагружения достаточно в полученной формуле приравнять фиктивную силу нулю:

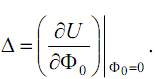
Таким образом, окончательно формула для определения перемещений упругой системы по методу нулевой силы выглядит следующим образом:

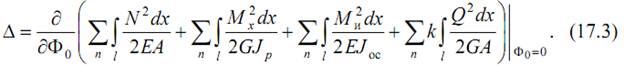
7.5. Метод Максвелла-Мора

Расчет по формуле (17.3) оказывается более удобным, если провести операцию дифференцирования непосредственно под знаком интеграла:

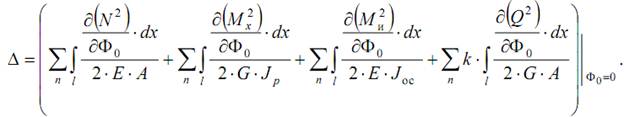
Вспоминая правила дифференцирования сложной функции, эту формулу можем переписать так

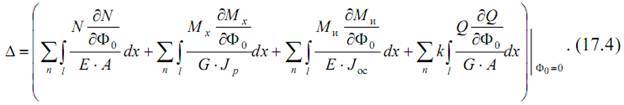
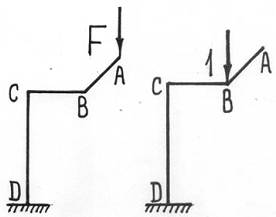
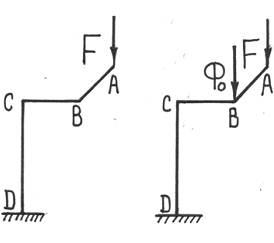Рассмотрим некоторую конструкцию, загруженную силой F в точке A. Пусть необходимо найти вертикальное перемещение ∆ в точке B. Чтобы воспользоваться формулой (17.4), приложим в точку B фиктивную силу Ф0 и исследуем полученную систему. Для того чтобы найти частные производные и упростить выражение (17.4), проведем следующие рассуждения, при этом будем пользоваться принципом независимости действия сил.

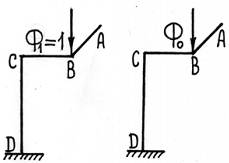1) Допустим, что в точке, где нам необходимо найти перемещение ∆, приложена фиктивная сила Φ1=1. Внутренние усилия, которые возникнут в балке от этой силы, обозначим

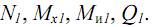
2) Очевидно, что если вместо силы Φ1=1 в ту же точку приложить какую-то другую силу Φ0, то внутренние усилия от силы Φ0 можно найти как

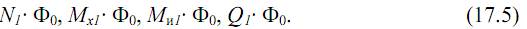
3) Внутренние усилия от внешних нагрузок (без учета фиктивной силы Φ0) обозначим следующим образом

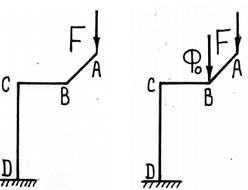Окончательно внутренние усилия в сечениях системы с учетом всех сил (внешних и фиктивной), приложенных к ней, определим, просуммировав усилия (17.5) и (17.6):

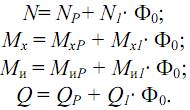
Теперь, для того чтобы воспользоваться формулой (17.4), необходимо взять частные производные от внутренних усилий, а затем приравнять фиктивную силу нулю (Φ0=0). Получим

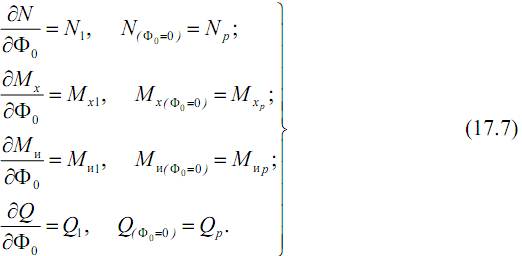
Подставляя зависимости (17.7) в формулу (17.4), окончательно получим выражение для расчета перемещений упругой системы по методу Максвелла-Мора в виде:

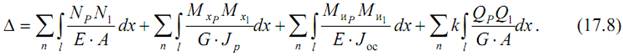
Таким образом, для того чтобы определить перемещения методом Максвелла-Мора, необходимо:

1) рассмотреть «грузовую» систему, нагруженную только внешними силами (без учета фиктивных сил), и записать для этой системы выражения для внутренних усилий по участкам;

2) рассмотреть «единичную» систему, нагруженную только одной силой – единичной силой Φ1=1, приложенной в том направлении и в той точке, где требуется найти перемещение, и записать для этой системы выражения

для внутренних усилий по участкам;

3) подставить найденные внутренние усилия в интеграл Максвелла-Мора (17.8) и найти перемещение.

Отметим, что для многих стержневых систем действием осевого усилия N и поперечных сил Q можно пренебречь. Тогда выражение (17.8) приводится к виду интеграла Мора, в котором учитываются только изгибающие и крутящие моменты, действующие на систему:

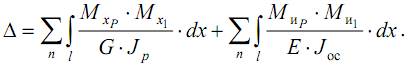
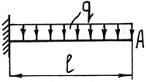Рассмотрим пример определения перемещений методом Максвелла-Мора. Пусть необходимо определить угловое перемещение ϕA свободного конца консольной балки длиной l, нагруженной распределенной силой q.

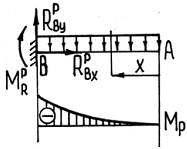Для определения перемещения необходимо рассмотреть две системы: 1) грузовую – нагруженную только внешними силами (нагрузка q и реакции от нее); 2) единичную – нагруженную единичной обобщенной силой, приложенной в точке и в направлении искомого перемещения (здесь также необходимо учитывать и реакции от этой силы). Так как нам необходимо найти угловое перемещение, то в качестве обобщенной единичной силы принимаем момент.

Применяя метод мысленных сечений, определим внутренние усилия, возникающие в сечениях каждой из систем:

а) грузовая система

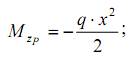
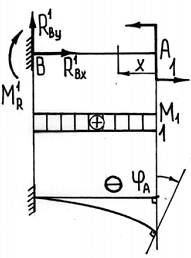б) единичная система

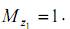
Подставим эти усилия в интеграл Максвелла-Мора и возьмем его

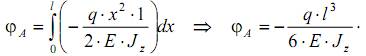
Здесь знак «минус» показывает, что найденное перемещение ϕA и единичный момент направлены в разные стороны.

17.6. Способ Верещагина

При исследовании изгиба стержневых систем оказывается удобным для определения перемещений использовать графо-аналитический метод, предложенный А. Н. Верещагиным (1924).

Так как при определении линейных или угловых перемещений единичная нагрузка будет представлять собой либо силу, либо момент, то эпюра внутреннего изгибающего момента для единичной системы всегда будет ограничена прямыми линиями. В этом случае интеграл Мора можно вычислить следующим образом.

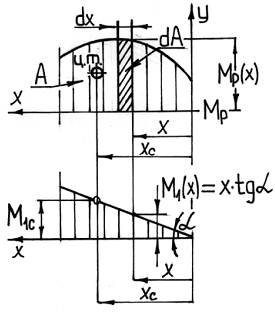Пусть «грузовая» эпюра MP имеет криволинейное очертание, а «единичная» эпюра M1 представляет собой наклонную прямую (с углом наклона α). На «грузовой» эпюре MP на расстоянии x от начала координат выделим элемент шириной dx. Площадь этого элемента, очевидно, равна dA=MP·dx. «Единичный» момент M1, соответствующий координате x, можно найти через тангенс угла α:

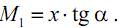
Запишем теперь интеграл Мора и подставим в него найденные соотношения:

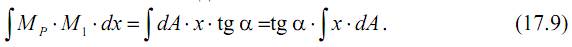
Выражение под знаком последнего интеграла есть ничто иное, как статический момент «грузовой» эпюры относительно оси Oy

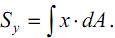
С другой стороны, статический момент можно найти как произведение площади на координату центра тяжести «грузовой» эпюры

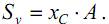
В этом случае интеграл (17.9) можно переписать так:

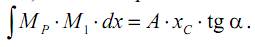
Произведение tg C x ⋅ α представляет собой величину единичного момента в точке с координатой xC:

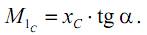
Таким образом, выражение для определения перемещения балки при изгибе по методу Верещагина запишем в следующем виде:

где А – площадь «грузовой» эпюры MP на данном участке; – величина «единичного» момента под центром тяжести «грузовой» эпюры на данном участке.

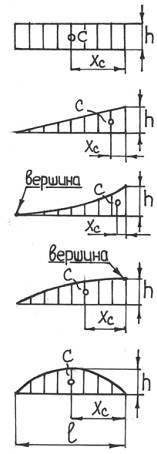Для удобства использования выражения (17.10) запишем формулы для определения площади и координаты центра тяжести для некоторых характерных эпюр:

В качестве примера рассмотрим консольную балку длиной l, нагруженную на конце силой F. Определим прогиб свободного края балки.

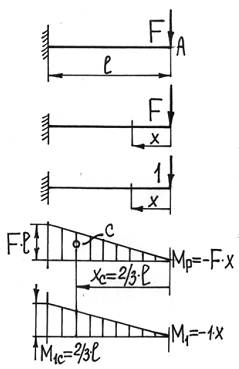Проанализируем две системы грузовую, – нагруженную только силой F, и единичную, – нагруженную единичной силой в направлении искомого перемещения.

Построим для каждой из систем эпюру внутреннего изгибающего момента (MP и M1).

Площадь «грузовой» эпюры найдем как

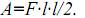
Значение «единичного» момента под центром тяжести «грузовой» эпюры определим из пропорции

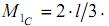
Тогда искомое перемещение

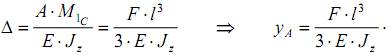
Знак «плюс» показывает, что направление перемещения совпадает с направлением единичной силы.

Дата добавления: 2014-01-14