Повышение точности

Оптимизация существенно улучшила характеристики системы. Но даже при оптимальном выборе коэффициентов усиления и обратной связи система не удовлетворяет заданным требованиям по точности. Уменьшим ошибку слежения до допустимой посредством добавления к входному сигналу его производной.

Рассмотрим произвольную замкнутую систему с единичной обратной связью. Пусть имеет место случай, когда на вход системы подается линейно-нарастающий сигнал f=vt, v=const. Тогда 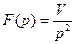и изображение сигнала ошибки ∆x(t) имеет вид:

. Примем, что возмущающее воздействие в системе отсутствует, тогда:

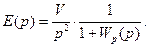
В нашем случае передаточная функция W_p(p) имеет астатизм 1-ог порядка, и может быть представлена виде:

,

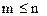
и при этом W^*(0)=1. Тогда в соответствии с теоремой о предельном значении:

()

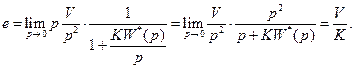Из () видно, что величина е установившейся ошибки пропорциональна скорости изменения задающего воздействия (его производной) и обратного пропорциональна коэффициенту передачи разомкнутой системы К.

Таким образом, чтобы избавится от установившейся ошибки, необходимо на вход системы подать сигнал пропорциональный производной входного сигнала 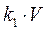. Коэффициент 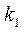подбирается в зависимости от структуры системы и приблизительно равен 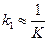, где K – коэффициент разомкнутой системы. Моделирование в среде MatLab показывает, что такой метод повышения точности вполне оправдан.

Продолжая рассуждения нетрудно предположить, что ошибка при гармоническом воздействии будет уменьшена до допустимого значения аналогичным образом. Чтобы вычислить коэффициент пропорциональности 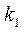, разложим производную входного сигнала в ряд Тейлора: …

Ограничимся первыми гармониками разложения:. Откуда может быть вычислен соответствующий коэффициент 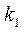. В нашем случае 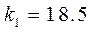. После этого проведем окончательную оптимизацию в NCD Blockset по всем четырем параметрам: К_у, К_ос, К_к, k₁. В результате получаем следующие значения коэффициентов: К_у= 170.77, К_ос= 20.97, К_к= 9.82, k₁= 21.05. После моделирования в среде Matlab, получаем следующие результаты.

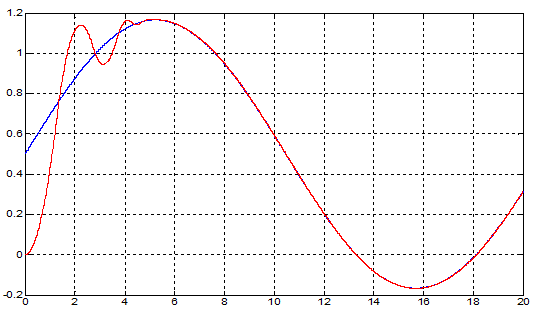
Рис.42. Переходный процесс после оптимизации коэффициентом при производной

(точный закон управления).

Из графиков видно, что данный закон управления обеспечивает необходимую точность слежения, но имеет колебательный переходный процесс.

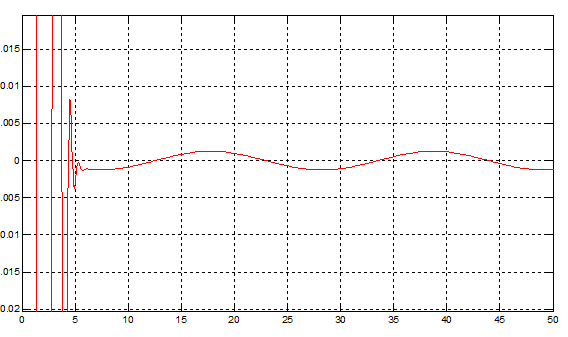
Рис.43 Ошибка слежения после оптимизации коэффициентом при производной

(точный закон управления).

Дата добавления: 2014-01-14