Синтез комбинированного управления

Принципиальная схема нечеткого регулятора, осуществляющего комбинированное управление электроприводом представлена на рис.44.

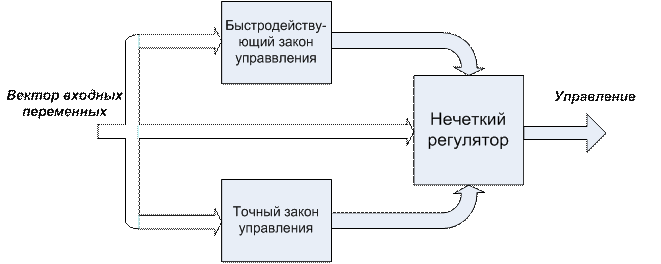
Рис.44. Принципиальная схема регулятора.

На вход регулятора поступает вектор входных переменных: величина ошибки слежения, скорость и значение производной входного сигнала. Величина ошибки является основным критерием выбора закона регулирования. Пока значение ошибки по положению велико работает быстродействующий закон управления, а когда положение вала двигателя оказывается близким к требуемым значениям, происходит плавное переключение на точный закон слежения. Основное назначение нечеткого регулятора – обеспечить как можно более плавный переход от одного закона управления к другому. Как уже говорилось выше, обеспечить такой переход классическими средствами не всегда возможно или, как правило, связано со значительными как вычислительными, так и техническими трудностями. В большинстве случаев в моменты переключения между законами управления в системе возникают различные нежелательные колебания, а также скользящие режимы, что крайне снижает показатели качества управления.

Фактически регулятор должен воспроизводить зависимость вида:

, где

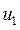- управление с выхода быстродействующего регулятора;

- управление с выхода регулятора, отрабатывающего точный закон управления;

- результирующее значение управления;

- коэффициент влияния на законы управления, который должен быть гладкой непрерывной функцией вектора входных переменных .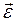

Рис.45. Структурная схема регулятора.

Структурная схема регулятора в среде Matlab состоит из пяти блоков: «Precision» - блок формирования точного закона слежения, «Fast» - формирователь быстродействующего закона, «Razdelitel» - блок, выделяющий из вектора входных переменных, необходимые для получения функции . Функция формируется нечетким контроллером в блоке «Fuzzy Logic Controller» и поступает на вход VS блока «FormUpr» вместе с сигналами управления с регуляторов «Fast» и «Precision». Блок «FormUpr» обеспечивает непосредственную реализацию зависимости . Остановимся на нем чуть подробнее.

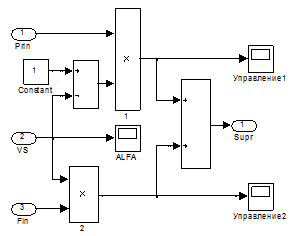
Рис.46. Структурная схема блока «FormUpr».

Нечеткий контроллер настроен таким образом, что функция может принимать значения только из интервала [0; 1]. Поэтому при больших значениях сигнала ошибки по положению на его выходе должна быть 1, а при точном слежении за входным сигналом – 0. Структура реализующая зависимость легко организуется с помощью двух умножителей и сумматоров и изображена на рис..

Из структурных схем регулятора видно, что во время работы системы задействованы одновременно оба закона управления, но доля их взаимного участия в процессе регулирования определяется нечеткой функцией .

Нечеткая функция состоит из двух лингвистических переменных: «ошибка слежения» и «коэффициент альфа», представленных рис. и таблицей.

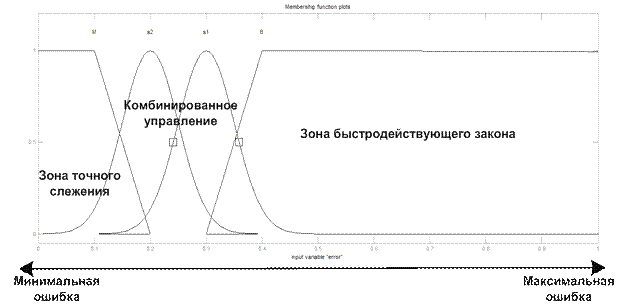
Рис.47. Лингвистическая переменная «Ошибка».

Лингвистическая переменная «коэффициент альфа»: Таблица 5

Функции принадлежности	Единичный B	Средний 1 S2	Средний 2 S1	Нулевой M
Коэффициент альфа		0.65	0.35

Параметры функций принадлежности выбирались достаточно произвольно, так как нет жестких правил, регламентирующих их выбор. Поэтому можно смело предположить, что работа нечеткого контроллера будет далека от оптимальной. Проведем оптимизацию параметров функции принадлежности с помощью генетических алгоритмов рассмотренными выше методами. Для этого по-прежнему будем использовать среду Matlab и редактор AnfisEdit. В качестве обучающей выборки возьмем следующую таблицу значений: Таблица 6

Значение ошибки		1.5		0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1	0.09	0.08	0.07	0.06	0.05	0.04	0.03
Значение α										0.9	0.8	0.7	0.6	0.5	0.4	0.2	0.1

Фактически нечеткий контроллер должен отрабатывать функцию, график которой изображен на рис. Разница между обычной функцией одной или нескольких переменных и нечеткой функцией заключается в том, что нечеткая функция не является однозначной, она зависит не от значений своих аргументов, а от оценок состояния входных величин. Поэтому невозможно описать жесткими математическими зависимостями физическую модель нечеткого контроллера. В этом и состоит его уникальность. Особенностью нейросети является именно то, что любой из её входов в разные моменты времени может быть охарактеризован различным состоянием сети, но это никак не отразится на общем её состоянии.

Рис.48. Характеристика обучающей выборки (желаемая характеристика).

Оптимизацию и обучение нейросети будет проводить методом обратного распространения ошибки на 100 шагах. Этого более чем достаточно для модели сети такой сложности. Как видно из графика сходимости поиск сходится уже на 12 шаге с вполне допустимой точностью.

Рис.49. Вид обучающей выборки и процесс обучения нейросети

Исследовав состояния лингвистических переменных можно даже невооруженным глазом заметить как нейросеть «поправила» параметры функций принадлежности. На рис. Изображены функции принадлежности лингвистической переменной «Ошибка» в исходном состоянии и после оптимизации нейросетью. Параметры лингвистической переменной «Коэффициент альфа» тоже изменились (См. Таблицу 7)

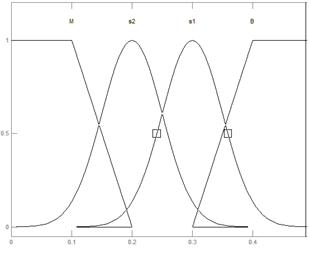
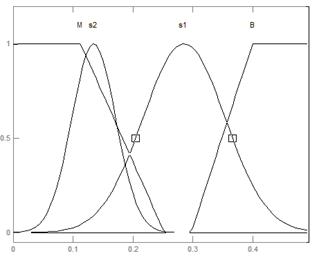
Рис.50 Лингвистическая переменная «Ошибка» до и после оптимизации нейросетью.

Таблица 7

Функции принадлежности	Единичный B	Средний 1 S2	Средний 2 S1	Нулевой M
Коэффициент альфа	1.001	1.927	0.9112	-0.01456

Промоделируем систему с комбинированным законом управления и нейронечетким контроллером в среде Matlab.

Рис.51. Структурная схема модели с нейронечетким контроллером.

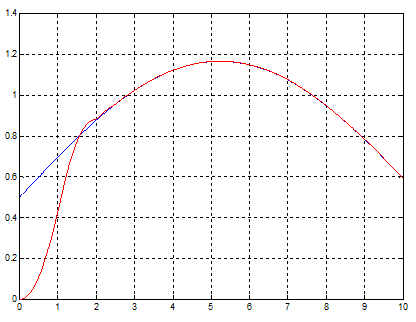
Рис.52 Переходный процесс в системе с комбинированным управлениеми и нейронечетким регулятором при гармоническом входном сигнале

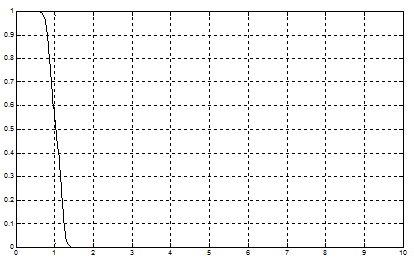
Рис.53 Характеристика величины 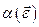на выходе нечеткого контроллера при гармоническом входном сигнале

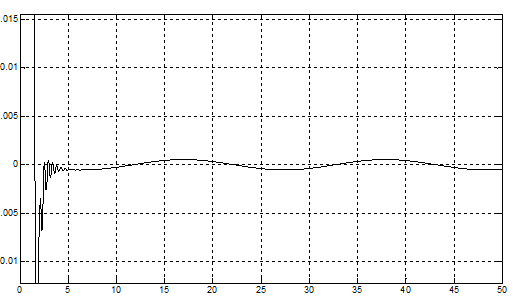
Рис.54 Ошибка слежения в системе с комбинированным управлениеми и нейронечетким регулятором при гармоническом входном сигнале

Рис.55 Сигналы управления с точного и быстродействующего регуляторов в системе с комбинированным управлениеми и нейронечетким регулятором при гармоническом входном сигнале

Дата добавления: 2014-01-14