Некоторые приёмы для вычисления

пределов последовательностей

Продемонстрируем на конкретных примерах.

1.

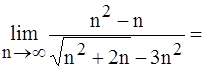
(делим числитель и знаменатель на «старшее слагаемое» n²)

= .

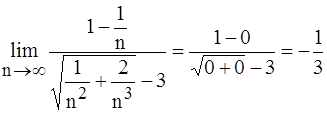2.

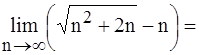
(умножим и разделим на «сопряжённое») =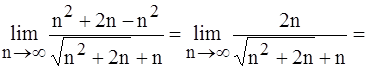

(разделим числитель и знаменатель на «старшее слагаемое» n)

3. (обозначая m = n/2) =

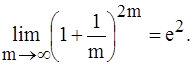
(Прокомментировать вольный переход к m).

4.

= (х = -) = =

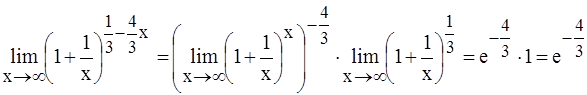
(Прокомментировать вольный переход к х).

5. .

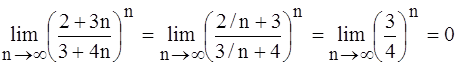§ 3. Предел функции одной переменной.

Пискунов Н.С. «Дифф…», 1966, т.1.,

гл.1, § 6, 7, 8, 9, стр. 17-28

гл.2, § 2, 3, стр. 31-38

п1. Введение.

Определение 1. Если каждому значению переменной х, принадлежащему некоторой области, соответствует одно определённое значение другой переменной у, то у есть функция от х, или в символической записи, у = f(x). Переменная х наз. независимой переменной или аргументом.

Определение 2. Совокупность значений х, для которых определяются значения функции у в силу правила f(x), наз. областью определения ( ОДЗ ).

Определение 3. Множество всех значений функции, которые она принимает в области определения, наз. областью значений.

Определение 4. f(x) наз. возрастающей (неубывающей), если большему значению х соответствует большее (не меньшее) значение f(x).

Аналогично определяются убывающие и невозрастающие функции. Говорят о монотонно возрастающих (или убывающих) на каком-либо отрезке или интервале функциях.

Определение 5. Если f(x) монотонно возрастает (или убывает) на отрезке [а,b] от значения C = f(a) до D = f(b), то на отрезке [C,D] определена обратная функция x = f ^–1(y), которая принимает значения от а до b.

Примеры:

1. y = sin(x), x = arcsin(y), -π/2 ≤ x ≤ π/2, -1 ≤ y ≤ 1.

2. y = x², x = √y, x ≥ 0, y ≥ 0.

3. y = e^x, x = ln(y), y ≥ 0, -∞ ≤ x ≤ ∞.

Способы задания функций (пояснить на примерах):

1. Табличный.

2. Графический.

3. Аналитический.

п2. Предел функции.

Определение 6. Пусть f(x) определена в некоторой окрестности точки х₀. Тогда число А наз. пределом f(x) в точке х₀ и обозначается , если такое, что для всех x таких, что | х – х₀ | < δ, выполнено неравенство | f(х) – A | < ε.

Пояснение. (см. рис. 1). Если А - предел f(x) в точке х₀, то для любой ε – окрестности точки А найдётся такая достаточно малая δ – окрестность точки х₀, что для любого х, взятого из δ – окрест-ности, соответствующее значение f(x) лежит в ε – окрестности точки А.

Y ε – окр.

f(x)

A

δ – окр.

х₀ х Х

Рис. 1.

Замечание. f(x) может быть не определена в точке х₀. Если же она определена в точке х₀, то f(x₀) может не совпадать с пределом А.

Определение 7. Если , то f(x) наз. непрерывной в точке х₀.

Определение 8. Число А наз. левосторонним (правосторонним) пределом f(x) в точке х₀, если в определении предела дополнительно указать, что х нужно брать только слева (справа) от точки х₀.

Односторонние пределы обозначают и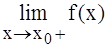

Ясно, что если в точке х₀ есть предел, то существуют и равны все три предела: левосторонний, правосторонний и просто предел.

Пример.

.

.

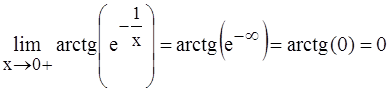(В точке х = 0 функция не определена).

Рис. 2.

Определение 9. Число А наз. пределом f(x) при х → ∞ (х → - ∞), если такое достаточно большое число В > 0 (достаточно большое по модулю число В < 0), такое, что для всех х > B (х < B) выполнено неравенство | f(х) – A | < ε.

Обозначение: .

Дата добавления: 2014-01-14