Наполнение полости постоянного объема через отверстие постоянной площади

Лекция 23.

В настоящем и последующих разделах рассмотрим практически важные случаи, когда удается найти аналитические решения дифференциальных уравнений, описывающих процессы в полости.

В начальный момент времени давление в полости равно , при открываются отверстия проточной площади 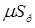и газ из источника, где и константы, начинает заполнять полость. Полагаем, рабочее тело является идеальным газом.

Изменение давления и плотности газа во времени определяется зависимостями

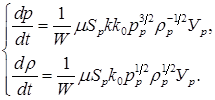
Пусть в начальный момент времени

, .

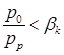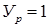В этом случае система легко интегрируется

,

,

.

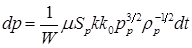Зависимости (3.12) и (3.12а) справедливы пока течение через впускной дроссель остается критическим, т.е. пока давление не достигнет уровня .

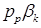Найдем время 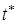, за которое давление в полости достигнет этого уровня.

,

.

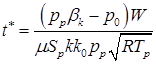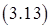
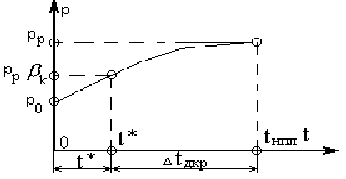
На участке наполнения, когда течение в полость остается критическим, давление по времени нарастает линейно.

При дальнейшем наполнении полости течение через впускной дроссель становится докритическим.

,

,

,

,

,

,

,

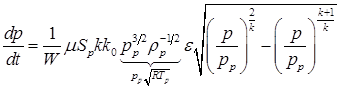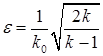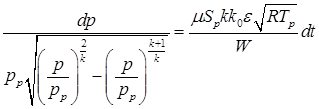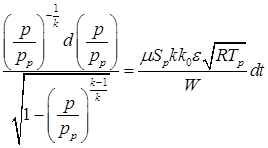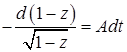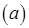
где .

Интегрируем зависимость (а) и переходим к исходным величинам

.

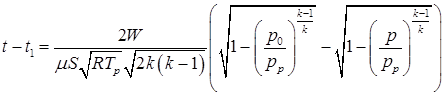(3.14) можно представить в виде , но формула в этом случае будет менее удобна для расчета.

Считая по формуле (3.14) задаемся величиной 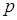и находим те значения интервала времени, за которое давление достигнет этого уровня.

В формуле (3.14) – давление, при котором начинает быть справедлива зависимость (3.14).

.

Полное время наполнения складывается из времени 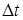, за которое давление в полости от начального значения достигнет уровня 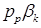и времени 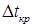, за которое давление от уровня 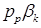достигнет уровня .

, ,

.

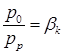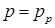Из (3.14) с учетом (*)

.

Получим далее формулы, связывающие с давлением плотность и температуру.

В системе (3.11) поделим первое уравнение на второе

,

.

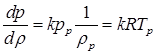Используя уравнение состояния 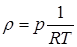, исключим из формулы (3.16) плотность и получим зависимость для температуры

.

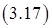
Зависимости (3.16) и (3.17) в сочетании с ранее полученными (3.12) и (3.14) позволяют рассчитать переходный процесс в полости по величинам 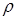и .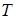

Анализируя (3.17) можно оценить характер и диапазон изменения температуры в полости наполнения. Для простоты и наглядности положим, что начальная температура в полости 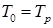. Тогда из (3.17)

.

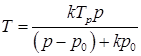Если при наполнении полости давление увеличилось незначительно, т.е. , то и температура, согласно формуле (3.17а), остается близкой к 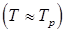. По мере увеличения давления 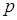, температура растет и достигает максимального значения при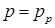

.

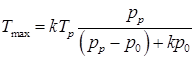Согласно формуле (3.17б) максимальная температура в полости тем больше, чем больше разность 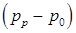. Предельное значение температуры в полости будет в том случае, если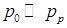

.

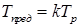Если наполняемая полость в начальный момент вакуумирована, то конечное значение температуры в ней не зависит от .

Дата добавления: 2014-01-14