Знакопеременные ряды. Абсолютная и условная сходимость

Интегральный признак сходимости Коши.

Теорема

Пусть члены ряда а₁+а₂+…+а_n –положительны и не возрастают а₁³а₂³…³а_n и пусть f(x) непрерывная возрастающая функция, такая что f(1)=a₁, f(2)=a₂, ….,f(n)=a_n тогда если 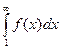сходится, то и ряд (1) сходится, если он расходится то и (1) расходится.

Рассмотрим ряд с членами произвольных знаков u₁+u₂+…+u_n=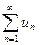(1). Ряд называется знакопеременным, если среди его членов есть как положительные, так и отрицательные при чем их расположение произвольно.

Рассмотрим одновременно ряд составленный из абсолютных величин ½u₁½+½u₂½+…+½u_n½=- (2).

Знакопеременный ряд (1) называется абсолютно сходящимся если сходится ряд (2) если же знакопеременный ряд (1) сходится а ряд два расходится то данный ряд (1) называется условно сходящимся.

Для знакопеременных рядов имеет место следующий достаточный признак сходимости.

Теорема 1

Если знакопеременный ряд таков, что ряд (2) сходится то и данный ряд (1) тоже сходится. Всякий абсолютно сходящийся ряд называется сходящимся рядом.

Замечание: Рассмотренная выше теорема (1) является достаточным, но не обходимым условием, так как существуют ряды которые сходятся, а ряды из абсолютных величин расходятся.

Теорема 2

Если ряд сходится абсолютно то он остается абсолютно сходящимся при любой перестановке его членов при этом сумма ряда не зависит от порядка членов, это свойство не сохраняется для условно сходящихся рядов.

Теорема 3

Если ряд сходится условно то какое бы ни было задано число А можно так переставить члены этого ряда, чтобы его сумма в точности стала равной А. И кроме того члены можно переставить так что ряд окажется расходящимся.

Дата добавления: 2014-01-14