Локальная форма уравнений

Уравнения массо-, тепло- и импульсоотдачи.

МЕЖФАЗНЫЙ ПЕРЕНОС СУБСТАНЦИЙ

Проведение основных процессов химической технологии сопровождаются переносом субстанций из ядра одной фазы через границу раздела в другую. В зависимости от вида переносимой субстанции можно выделить массо-, тепло-, импульсопередачу. Возможен одновременный межфазный перенос нескольких субстанций. Например, при прохождении струи газа сквозь слой жидкости, не находящейся в условиях концентрационного равновесия с ним и обладающей отличной температурой, будет одновременно осуществляться массо-, тепло- и импульсопередача.

В процессе межфазного переноса субстанции можно выделить три стадии: перенос субстанции от ядра первой фазы к границе раздела фаз, перенос непосредственно через границу раздела фаз и перенос от границы раздела фаз к ядру второй фазы. Перенос от границы раздела фаз к ядру фазы или от ядра к границе в зависимости от вида субстанции называют массо-, тепло- или импульсоотдачей.

При решении инженерных задач, зачастую, не требуется знания полей скорости, давления, температуры, концентраций, а также потоков субстанций во всем объеме аппарата. Достаточно получить значения скорости, давления, температуры и концентраций компонентов в каждой из фаз на выходе из аппарата, при заданных, как правило, входных величинах. Это можно сделать с помощью законов сохранения массы, импульса и энергии в интегральной форме, зная количество субстанций, перенесенных из одной фазы в другую. Для определения последних применяются уравнения межфазного переноса субстанций, в локальной и интегральной формах.

Таким образом, в инженерной практике решение системы дифференциальных уравнений в частных производных, составляющих исчерпывающее описание процессов переноса, заменяется решением системы линейных алгебраических уравнений баланса субстанций и межфазного переноса, что является существенным упрощением. Однако теоретическое определение коэффициентов в уравнениях межфазного переноса субстанций, вывод самих уравнений и их грамотное применение возможны лишь на основе исчерпывающего описания процессов переноса.

Инженеру требуются понимание сути происходящих процессов, умение их анализировать, находить качественно новые решения, что невозможно без усвоения теоретических основ.

Рассмотрим элементарный, бесконечно малый участок межфазной поверхности dF. Прямоугольную систему координат расположим так (рис.7), чтобы плоскость X - Z совмещалась с поверхностью раздела фаз, а ось Х с направлением движения рассматриваемой фазы (поскольку участок межфазной поверхности выбран бесконечно малым, его можно считать плоским).

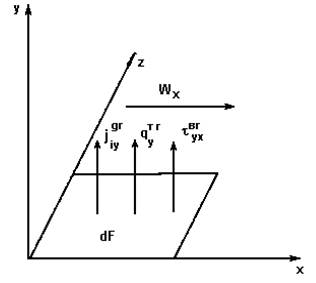
Рис. 7. Перенос субстанций через элементарный участок межфазной поверхности dF.

Поток субстанций через границу раздела фаз будет осуществляться по нормали к ней, т.е. вдоль оси Y. Рассмотрим потоки субстанций за счет молекулярного и турбулентного механизмов переноса, которые будем называть в зависимости от вида соответствующих коэффициентов переноса диффузионным потоком массы 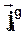, вязким потоком импульса 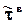(тензор вязких напряжений), потоком тепла за счет теплопроводности 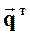. В отличие от полных потоков данные величины не учитывают конвективный механизм переноса субстанций несмотря на то, что он может присутствовать. Продемонстрируем вывод уравнений на примере теплоотдачи. Проекция теплового потока за счет теплопроводности на ось Y будет иметь вид

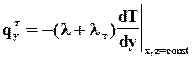. (89)

Введем величину q*(y), характеризующую отношение потока на расстоянии y от межфазной границы к граничному значению

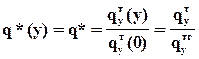. (90)

С использованием величины q* перепишем уравнение (89), решим его относительно dT и проинтегрируем, используя модель пограничного слоя, от границы раздела фаз до внешней границы слоя (d_т). Температура при этом изменится от значения на межфазной поверхности (Т^г) до значения в ядре фазы (Т^я). Следует иметь ввиду, что коэффициент турбулентной теплопроводности является функцией расстояния от границы раздела фаз l_т(y) и не может быть вынесен из под интеграла. 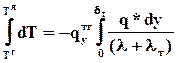. (91)

Решив уравнение (91) относительно q_у^тг, получим уравнение теплоотдачи. Выражение в его правой части, стоящее перед разностью температур, носит название коэффициента теплоотдачи 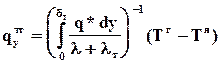. (92)

Аналогичным образом могут быть получены уравнения массо- и импульсоотдачи, что позволяет использовать единую форму их представления и определить соответствующие коэффициенты

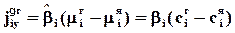, (93) 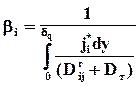,(96)

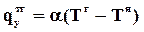, (94) 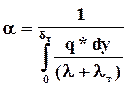, (97)

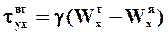, (95) 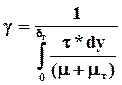,(98)

здесь j_iy^gг, q_y^тг, t_yx^вг - потоки вещества компонента i, тепла и импульса через границу раздела фаз без учета конвективных составляющих; b_i или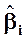, a,g - коэффициенты массо-, тепло- и импульсоотдачи соответственно; m_i^я, c_i^я, Т^я, W_x^я - значения химического потенциала, концентрации компонента i, температуры, скорости в ядре фазы; m_i^г, c_i^г, Т^г, W_х^г - значения этих величин для данной фазы в непосредственной близости от границы раздела фаз. dд, d_т, d_г - толщины диффузионного, теплового и гидродинамического пограничных слоев.

Как правило, конвективный перенос субстанций через границу раздела фаз отсутствует и j_iy^тг, q_y^тг, t_yx^тг представляют собой полные потоки. Однако и в этом случае внутри пограничного слоя может осуществляться конвективный перенос в направлении оси Y. Для нахождения полного потока при y ¹0 к соотношениям типа (89) необходимо добавлять конвективную составляющую, например, rc_рTW_у

При наличии конвективного переноса субстанций через границу раздела фаз его необходимо учитывать дважды, во-первых, добавляя конвективные члены при определении полного потока к уравнениям и, во-вторых, вводя поправки к коэффициентам массо-, тепло-, и импульсоотдачи, найденным в отсутствии конвективного переноса через межфазную границу (учет так называемых эффектов "вдува" или "отсоса").

Разница значений химических потенциалов или концентраций, температур, скоростей у границы раздела фаз и в ядре фазы носит название движущей силы массо-, тепло- и импульсоотдачи. Отличие ее от нуля является необходимым условием протекания соответствующего процесса. Смысл коэффициентов легко понять, решив относительно них эти уравнения

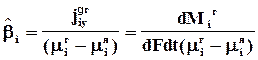, моль²/Дж м²с (99)

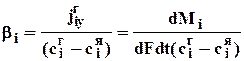, м/с (100)

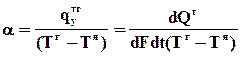, Вт/м²К (101)

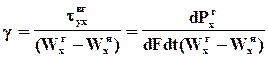, кг/м²с (102)

Коэффициент массоотдачи b- количество вещества компонента i, переносимое от границы раздела фаз в ядро фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности в расчете на единицу движущей силы. Рассмотренные уравнения справедливы для двухкомпонентных сред. В случае многокомпонентных систем должны использоваться матрицы коэффициентов массоотдачи.

Коэффициент теплоотдачи a характеризует количество тепла, переносимое от границы раздела фаз к ядру фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности в расчете на единицу движущей силы.

Коэффициент импульсоотдачи g характеризует количество импульса Р_x, переносимое от границы раздела фаз к ядру фазы или в обратном направлении за единицу времени, через единицу межфазной поверхности в расчете на единицу движущей силы.

При межфазном переносе субстанций не всегда можно воспользоваться моделью пограничных слоев. Так, при ламинарном течении в трубе профиль продольной скорости W_х имеет параболическую зависимость, в случае пленочной конденсации пара профиль температур в пленке изменяется линейно по всей толщине, что делает бессмысленным выделение ядра потока, в котором происходит лишь 1% изменения соответствующей величины. В этом случае, как правило, вместо значения переменной в ядре потока в уравнениях используют ее значение, усредненное по поперечному сечению. При этом будут изменяться и величины кинетических коэффициентов, условимся обозначить их в этом случае b_i¢, a¢, g¢. Поэтому при применении уравнений массо-, тепло- и импульсоотдачи необходимо убедиться, что соответствующие коэффициенты определены при использовании идентичных движущих сил.

Дата добавления: 2014-01-14