
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Движение сред через слои зернистых материалов и насадок
|
|
|
|
Размеры пузыря, отрывающегося от отверстия. При небольших скоростях истечения легкая фаза вытекает в виде последовательно отрывающихся пузырей (капель). В общем случае на образующийся пузырь воздействует подъемная сила и конвекционные токи жидкости, стремящиеся оторвать пузырь от кромки отверстия. Сила, прижимающая пузырь к кромке отверстия, пропорциональна коэффициенту поверхности натяжения и периметру отверстия pd1s.
Образование и движение газовых пузырей и капель
Диспергирование газов и жидкостей, т.е. образование газовых пузырей и жидких капель в сплошной фазе широко используется в процессах физического и химического взаимодействия между этими средами (газ-жидкость, жидкость-жидкость), в основном, для увеличения поверхности контакта фаз. Во всех случаях необходимо знать размеры, частоту образования и закономерности движения пузырей и капель.
Диспергирование газов в жидких средах. Диспергирование происходит при истечении газов из сопел или отверстий в плоских или криволинейных стенках газораспределительных устройств. Различают два режима истечения: свободный и цепочный. Первый наблюдается при малых расходах газа и характеризуется определенным расстоянием между всплывающими пузырями, т.е. каждый новый пузырь образуется после того, как предыдущий уже прошел некоторый путь. Второй режим проявляется при больших расходах газа. В этом случае происходит быстрое образование пузырей так, что вблизи отверстия они касаются друг друга, образуя как бы цепочку. При дальнейшем увеличения расхода газа из отверстия (сопла) в жидкость истекает уже струя, которая в последующем распадается на отдельные пузыри. При этом в струе газа при воздействии ее на жидкость, могут появляться и капли жидкости.
Диспергирование капельных жидкостей в газовых средах и в объемах других не смешивающихся жидкостей. Возможны два режима диспергирования при истечении: капельный и струйный. В первом случае капли образуются непосредственно при истечении жидкости из отверстия или сопла. Во втором случае струя распадается на капли на некотором расстоянии от выходного сечения диспергирующего устройства.
Другим способом диспергирования жидкостей, обеспечивающим большую однородность размера капель, является отрыв пленки жидкости от вращающихся дисков или цилиндров под действием центробежной силы. Ещё один способ диспергирования одной жидкости в другой при их взаимной нерастворимости заключается в перемешивании с помощью механических.
При слабых конвекционных токах в момент отрыва имеем:
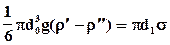 (93)
(93)
где d0 - диаметр пузыря в момент отрыва, d1 - диаметр отверстия, r¢, r¢¢ - плотности тяжелой и легкой фазы, соответственно.
Из уравнения (93) определяем d0: 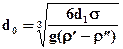 (94)
(94)
При увеличении объемного расхода газа через отверстие частота отрыва единичных пузырей возрастает и достигает критического значения, при котором начинается цепочное движение пузырей. Критическое значение расхода
через отверстие частота отрыва единичных пузырей возрастает и достигает критического значения, при котором начинается цепочное движение пузырей. Критическое значение расхода  может быть найдено из следующих соображений. Всплывающие со скоростью Wn пузыри выстраиваются в вертикальную цепочку, среднее сечение которой соответствует гипотетическому цилиндру эквивалентного объема
может быть найдено из следующих соображений. Всплывающие со скоростью Wn пузыри выстраиваются в вертикальную цепочку, среднее сечение которой соответствует гипотетическому цилиндру эквивалентного объема
При цепочном движении размер пузырей увеличивается с возрастанием расхода газа 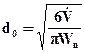 (95)
(95)
Движению капель и пузырей, в отличие от движения твердых сфер, присущ ряд характерных особенностей. На жидкой границе раздела фаз касательная составляющая скорости отлична от нуля, вследствие чего внутри движущейся капли (пузыря) возникает циркуляция среды, способствующая лучшему обтеканию капли по сравнению с обтеканием твердой сферы. Это означает, что для капли отрыв пограничного слоя наблюдается при более высоких значениях Re, чем для твердой сферы, и скорость осаждения капли (пузыря) выше скорости осаждения твердой сферы того же диаметра. Вместе с тем, ввиду подвижности границы раздела фаз, капли (пузыри) могут деформироваться и колебаться при своем движении.
Скорость движения капли и пузырька при R < 1. Для капли, движущейся в жидкости под действием подъемной силы скорость ее установившегося движения (падение или всплытие) определяется по формуле:
 (96)
(96)
где m¢¢ - динамической вязкости сплошной фазы и m ¢¢ - динамической вязкости дисперсной фазы.
Движение капель и пузырей при R > 1. Увеличение диаметра пузырей и капель приводит к их деформации, они уже не могут считаться сферическими, траектории движений отличаются от вертикалей, и соотношения для определения скорости их движения не удается получить теоретически. При достаточно больших скоростях движения капель относительно сплошной фазы они могут разделяться (дробление), а при соударениях сливаться (коалесценция).
Массовый барботаж. Выше рассматривалось образование и всплытие пузырей от единичного отверстия. На практике широко используется массовый барботаж - прохождение газа в жидкость через множество отверстий, например, в тарельчатых колоннах. При малых расходах газа в режиме всплытия отдельных пузырьков к ним применимы закономерности полученные ранее. Однако при увеличении расхода газа, когда происходит стесненное движение пузырей, данные закономерности нарушаются. При дальнейшем увеличении расхода газа образуется слой пены. Еще большее увеличение расхода газа приводит к разрушению слоя пены и газ проходит сквозь жидкость в виде струй.
Для характеристики газожидкостного слоя при массовом барботаже используются такие величины как газосодержание  , высота слоя hс, высота светлого слоя жидкости h0. Газосодержание характеризует объемную долю газа в газожидкостном слое. Высота светлого слоя жидкости характеризует количество жидкости в газожидкостном слое и представляет собой гипотетическую высоту слоя при его нулевом газосодержании
, высота слоя hс, высота светлого слоя жидкости h0. Газосодержание характеризует объемную долю газа в газожидкостном слое. Высота светлого слоя жидкости характеризует количество жидкости в газожидкостном слое и представляет собой гипотетическую высоту слоя при его нулевом газосодержании
 (97)
(97)
Расчет величин  и h0 проводится, как правило, по эмпирическим соотношениям.
и h0 проводится, как правило, по эмпирическим соотношениям.
Слои зернистых материалов могут состоять из частиц одинакового (монодисперсный слой) и различных диаметров (полидисперсный слой). Зернистый слой, в частности, характеризуется размером его частиц, удельной поверхностью и долей свободного объема.
Удельная поверхность а (м2/м3) представляет собой поверхность частиц находящихся в единице объема, занятого слоем.
Доля свободного объема, или порозность e, выражает объем свободного пространства между частицами в единице объема, занятого слоем.
Обозначим: V - общий объем, занимаемый зернистым слоем, V0 - объем, занимаемый самими частицами, образующими слой, тогда
 (98)
(98)
Пусть в объеме слоя V имеется N частиц. Объем самих частиц V0 равен V(1- e), а их поверхность V×а. Средний объем одной частицы
 (99)
(99)
а ее поверхность  (100)
(100)
где d - диаметр эквивалентного шара, имеющего тот же объем, что и частица; Ф = Fш/Fr - фактор формы; Fш - поверхность шара, имеющая тот же объем, что и рассматриваемая частица с поверхностью Fr. Для сферических частиц Ф = 1.
Отношение поверхности частицы к ее объему будет:
 откуда
откуда  (101)
(101)
Среда в зернистом слое движется по каналам, образованным твердыми частицами. Эквивалентный диаметр dэ, соответствующий суммарному поперечному сечению каналов в зернистом слое, можно определить следующим образом. Если площадь поперечного сечения аппарата, заполненного зернистым слоем, составляет S (м2), а высота равна Н (м) (рис.18), то объем слоя V = SH и объем самих частиц V0 = SH(1- e), а свободный объем слоя Vсв = SHe Поверхность частиц, равная поверхности образуемых ими каналов, составляет SHa.
Для того, чтобы определить суммарное сечение каналов слоя, или свободное сечение слоя, надо разделить свободный объем слоя Vсв на длину каналов. Однако длина их неодинакова и должна быть усреднена. Если средняя длина каналов, превышает высоту слоя в ak раз, то средняя длина каналов равна akН, а свободное сечение слоя Sсв составляет Sсв = SHe/akН = Se/ak, где ak - коэффициент кривизны каналов. Смоченный периметр свободного сечения слоя Пс может быть вычислен делением общей поверхности на их среднюю длину, т.е.
 (102)
(102)
Следовательно, эквивалентный диаметр каналов зернистого слоя выразится отношением  (103)
(103)

Рис.18 Вертикальный цилиндрический аппарат, заполненный зернистым слоем.
Подставляя величину а, получим зависимость dЭ от размера частиц
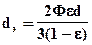 (104)
(104)
Для полидисперсных зернистых слоев средний диаметр частиц dср вычисляют из соотношения 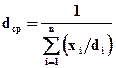 (105)
(105)
где xi- объемная или, при одинаковой плотности, массовая доля частиц с диаметром d i.
Гидравлическое сопротивление слоя (потерянное давление) можно определить по уравнению, аналогично для прямолинейного участка трубы
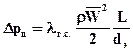 (106)
(106)
где lг.с- фиктивный коэффициент трения, обычно называемый в случае зернистого слоя коэффициентом гидравлического сопротивления, учитывающий как потери энергии на трение, так и все местные сопротивления (изгиб каналов, обтекание частиц, изменение формы сечения каналов и т.д.);  - действительная средняя скорость движения жидкости в каналах.
- действительная средняя скорость движения жидкости в каналах.
Для определения действительной скорости  , вначале находят фиктивную скорость жидкости
, вначале находят фиктивную скорость жидкости  , равную отношению объемного расхода жидкости к площади поперечного сечения аппарата, а далее на основании уравнения неразрывности S
, равную отношению объемного расхода жидкости к площади поперечного сечения аппарата, а далее на основании уравнения неразрывности S  = Sсв
= Sсв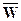 = Se
= Se  , находят значение действительной скорости
, находят значение действительной скорости 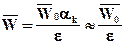 (107)
(107)
при этом считают, что ak= 1, т.е. длина каналов L равняется высоте слоя Н, т.е. L = Н. На самом деле величина  меньше скорости жидкости в каналах, т.к. ak > 1. Поскольку lг.с определяется опытным путем, то допущение L = Н мало влияет на величину DРn, то
меньше скорости жидкости в каналах, т.к. ak > 1. Поскольку lг.с определяется опытным путем, то допущение L = Н мало влияет на величину DРn, то
 (108)
(108)
Коэффициент сопротивления lг.с зависит от гидродинамического режима движения среды в слое, определяемого по величине числа Рейнольдса. В данном случае после подстановки  и dэ выражение числа Рейнольдса принимает вид:
и dэ выражение числа Рейнольдса принимает вид:
 (109)
(109)
где  - массовая скорость жидкости, кг/(м2с).
- массовая скорость жидкости, кг/(м2с).
Для определения lг.с для всех режимов движения рекомендуется уравнение
 (110)
(110)
При движении жидкости (газа) в зернистом слое турбулентность потока развивается значительно раньше, чем при течении по трубам, причем между ламинарным и турбулентным режимами нет резкого перехода. Ламинарный режим практически существует примерно при Re < 50.
Порозность и удельная поверхность контакта фаз зернистых материалов, как правило, невелика. Для увеличения поверхности контакта газовой и жидкой фаз в аппарат загружают специально изготовленную насадку, элементы которой представляют собой твердые достаточно крупные тела сложной формы.
Величина порозности e зависит от соотношения между диаметром частиц d и диаметром аппарата D, в котором находится зернистый слой. Это связано с так называемым пристеночным эффектом: порозность слоя у стенок всегда выше, чем в центральной части слоя. Указанное различие порозности тем значительнее, чем больше отношение d/D.
Движение среды через неподвижный зернистый слой называется фильтрацией.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 1317; Нарушение авторских прав?; Мы поможем в написании вашей работы!