Начальные и центральные моменты

Рассмотрим дискретную случайную величину , заданную законом распределения:

X	-150
P	0,02	0,18	0,6	0,2

Найдем математическое ожидание M(X). Имеем:

.

Составим ряд распределения для случайной величины :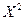

X^2
P	0,02	0,18	0,6	0,2

Математическое ожидание 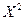равно:

.

Видим, что 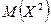значительно больше 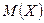. Это можно объяснить тем, что значение x = –150, намного отличающееся от остальных значений, при возведении в квадрат резко возросло; вероятность же этого значения мала (0,02). Таким образом, переход от M(X) к M(X²) позволил лучше учесть влияние на математическое ожидание таких значений случайной величины, которые велики по абсолютной величине, но вероятность их появления мала. Разумеется, если бы величина имела несколько больших и маловероятных значений, то переход к величине X², а тем более к величинам , 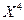и т.д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины, причем не только дискретной, но и непрерывной.

Определение 6.10. Начальным моментом го порядка случайной величины называется математическое ожидание величины :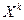

(6.20)

В частности:

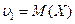, (6.21)

Пользуясь этими моментами, формулу для вычисления дисперсии можно записать иначе

(6.22)

Кроме моментов случайной величины целесообразно рассматривать моменты отклонения .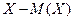

Определение 6.11. Центральным моментом ого порядка случайной величины называется математическое ожидание величины .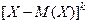

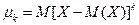(6.23)

В частности,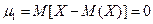

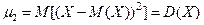(6.24)

Легко выводятся соотношения, связывающие начальные и центральные моменты. Так, сравнивая (6.22) и (6.24), получим:

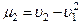(6.25)

Нетрудно доказать и следующие соотношения:

.

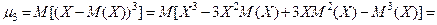
Аналогично:

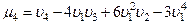(6.26)

Моменты более высоких порядков используются редко. В определении центральных моментов используются отклонения случайной величины от ее математического ожидания (центра). Поэтому моменты называются центральными.

В определении начальных моментов также используются отклонения случайной величины, но не от математического ожидания, а от точки, абсцисса которой равна нулю, являющейся началом координат. Поэтому моменты называются начальными.

В случае непрерывной случайной величины начальный момент го порядка вычисляется по формуле:

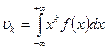(6.27)

Центральный момент го порядка непрерывной случайной величины вычисляется по формуле:

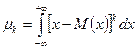(6.28)

Предположим, что распределение случайной величины симметрично относительно математического ожидания. Тогда все центральные моменты нечетного порядка равны нулю. Это можно объяснить тем, что для каждого положительного значения величины X-M(X) найдется (в силу симметричности распределения относительно M(X)) равное ему по абсолютной величине отрицательное значение этой величины, причем их вероятности будут одинаковыми.

Если центральный момент нечетного порядка не равны нулю, то это говорит об асимметричности распределения, причем чем больше момент, тем больше асимметрия. Поэтому в качестве характеристики асимметрии распределения разумнее всего взять какой-нибудь нечетный центральный момент. Так как центральный момент первого порядка всегда равен нулю, то целесообразно для этой цели использовать центральный момент третьего порядка.

Определение 6.12. Коэффициентом асимметрии 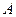называется величина:

(6.29)

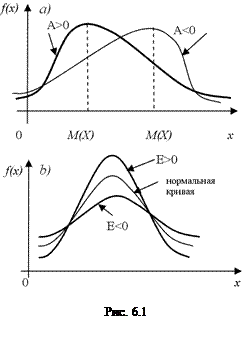
Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину отрицательных отклонений. В этом случае кривая распределения (рис. 6.1 а) более полога слева от 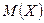. Если коэффициент 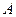положительный, а значит, преобладает влияние положительных отклонений, то кривая распределения более пологая справа.

Как известно, второй центральный момент (дисперсии) служит для характеристики рассеивания значений случайной величины вокруг ее математического ожидания. Если этот момент для некоторой случайной величины достаточно большой, т.е. рассеивание велико, то соответствующая кривая распределения более пологая, чем кривая распределения случайной величины, имеющей меньший момент второго порядка. Однако моментне может служить для этой цели в силу того, что для любого распределения .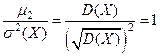

В этом случае используется центральный момент четвертого порядка.

Определение 6.13. Эксцессом называется величина:

(6.30)

Для наиболее распространенного в природе нормального закона распределения отношение . Поэтому эксцесс, заданный формулой (6.28) служит для сравнения данного распределения с нормальным (рис. 6.1 b).

Дата добавления: 2014-01-14