Небесная сфера. Горизонтная сис-ма

Небесной сферой называется вспомогательная сфера произвольного ра­диуса, к центру которой параллельно перенесены основные линии наблюда­теля и Земли и направления на светила.

Основным направлением наблюдателя М является его вертикаль, или отвесная линия, zО₁ (см. рис. 1), положение которой в данной точке Земли по­стоянно и определяется направлением силы притяжения. Пересечение вер­тикали с поверхностью Земли представляет место М наблюдателя. Положе­ние точки М на Земле определяется ее географической широтой φ (угол между отвесной линией и плоскостью экватора) и долготой λ (двугранный угол между меридианами — гринвичским Гр и наблюдателя М, равный дуге е_ое). Введение небесной сферы позволяет построить аналогичные системы координат для светил.

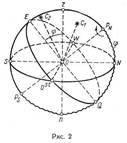
При построении небесной сферы ее центр выбирают в произвольной точ­ке О (рис. 2) и через нее проводят линии, параллельные линиям наблюдателя М (см. рис. 1, б). Линия, параллельная вертикали zО₁ называется отвесной линией zn, а точки пересечения ее со сферой — зенитом z и надиром п. Линия, параллельная оси р_пр Земли (см рис. 1, а), представляет на сфере ось мира PnPs, вокруг которой вращается сфера. Точки пересечения ее со сферой на­зываются полюсами мира: северным Pn и южным Ps (они соответствуют по­люсам Земли).

Плоскость Н истинного горизонта наблюдателя М (см. рис. 1, а), про­веденная через центр сферы, дает в сечении со сферой истинный горизонт — большой круг NOstSW, перпендикулярный отвесной линии zn.

Плоскость экватора Земли, перенесенная к центру О сферы дает в се­чении со сферой небесный экватор — большой круг EWQO^st, плоскость которого перпендикулярна оси мира.

Плоскость p_nMep_s (см. рис. 1, а) — географического меридиана наблю­дателя М, проведенная через центр сферы, дает в сечении с ней меридиан наблюдателя — большой круг PnzEPsQ Ось мира PnPs разделяет мери­диан наблюдателя на полуденную часть PnzPs, включающую зенит, и по­луночную PNnPs (на рис. 2 волнистая линия). Эти части меридиана Солнце пересекает в полдень и в полночь, отсюда их названия.

Основные круги сферы делят ее на части: горизонт — на надгоризонтную и подгоризонтную, где светила не видны: небесный экватор — на северную (Pn) и южную (P_s); меридиан наблюдателя NzS — на восточную (O^st) и западную (W).

Истинный горизонт наблюдателя делится на направления (румбы). Пересечение плоскостей меридиана и горизонта дает полуденную линию N—S, а плоскостей экватора и горизонта — линию O^st — W. На сфере пересе­чение этих линий дает точки N, О', S, W, которыми горизонт разделяется на четыре четверти: NO, SO, SW, NW. Кроме того, горизонт делится на гра­дусы (можно представить его в виде картушки компаса).

Полюс мира, расположенный над горизонтом, называется повышенным полюсом. Его наименование совпадает с широтой наблюдателя: в северной широте — Pn, в южной — Ps- Возвышение полюса над горизонтом, т. е. дуга NP_N, равно широте, так же как дуга zE (см. рис. 2).

Если из центра сферы провести направления на светила, то на ее по­верхности получаются точки С₁ С₂, называемые видимыми местами светил (в дальнейшем просто светила). На сферу можно также спроектировать и другие плоскости и объекты: плоскость орбиты Земли даст эклиптику, орби­ты Луны — видимую орбиту Луны, орбиты спутника — видимую орбиту спутника и т. п.

Горизонтная система координат. Основными кругами (осями коорди­нат) в этой системе являются истинный горизонт и меридиан наблюдателя; основным направлением — отвесная линия zп. Положение точки или свети­ла на сфере определяется двумя координатами: высотой и азимутом (рис. 4; сфера на нем для φ_N повернута W-м к зрителю).

Высотой_h__светила называется дуга его вертикала от истинного горизонта до места светила. Угол при центре сферы, измеряющий эту дугу, также называют высотой. Этот угол измеряется при наблюдениях. Высоты счи­таются в пределах от 0 до ±90° с «+» над горизонтом, с «—» под горизонтом» например светило С₁ имеет h = 46°, светило С’₁ — h = —30°; высота зени­та +90°, надира —90° и т. п.

Азимутом А светила называется дуга истинного горизонта между ме­ридианом наблюдателя и вертикалом светила. Эта дуга измеряет плоский угол при центре сферы или сферический угол А при зените, которые поэтому также называют азимутами.

В мореходной астрономии применяют три системы счета азимутов: полукруговой, круговой и четвертной.

Полукруговой азимут считается в пределах 0—180° от полуночной части меридиана наблюдателя или от вертикала повышенного полюса в сторону Оst-а или W-a до вертикала светила, например А = N100°W (см. рис. 4). В северной широте начальной точкой счета является N, в южной — S, по­этому первая буква наименования азимута совпадает с широтой, вторая — с половиной сферы, где расположено светило. Этот счет азимутов приме­няется при решении сферических треугольников по формулам и по таблицам ВАС—58.

Круговой азимут считается от точки N в сторону O^st-a до вертикала светила в пределах 0—360°, т. е. совпадает с истинным пеленгом светила, например для светила С₁ А = ИП = 260^Q. Этот счет применяется при опре­делениях ∆К и при прокладке.

Четвертной азимут считается по четвертям — от ближайшей части меридиана наблюдателя до вертикала светила в пределах 0—90°, например светило С₁ имеет А = 80° SW. Этот счет применяется в формуле синусов и ТВА—57. Необходимо уметь свободно переходить от одной системы счета азимута к другим — это постоянно требуется на практике. Например, для светила С₂ (см. рис. 4) имеем: полукруговой А = N150° O^st; круговой А = = 150°; четвертной А = 30°SO. Положение светила С₁ в горизонтной си­стеме запишется так: А = 260°; h = 46°. Одна горизонтная координата оп­ределяет на сфере положение одного круга: азимут — положение верти­кала, высота — альмукантарата.

Полярные координаты. Положение точки на сфере может быть определе­но и без построения горизонта — непосредственно при зените. Зенит яв­ляется полюсом, а меридиан наблюдателя — полярной осью координат Лиг. Азимут в полярных координатах определяется как угол при зените в полу­круговом счете (см. рис. 4).

Зенитным расстоянием z называется дуга вертикала от зенита до места светила в пределах 0 — 180^е. Зенитное расстояние связано с высотой соот­ношением

Z = 90° — h. (1)

Дуга z измеряет центральный угол z между отвесной линией и направ­лениями на светила (этот угол измеряется береговыми инструментами). Полярные координаты применяются при решении сферических треуголь­ников.

Меридиональная высота. Высота светила, расположенного на меридиане наблюдателя, называется меридиональной высотой Н. Ей придается наи­менование той точки горизонта, над которой она измерена, например для С₃ Н = 35° S. Наименование меридионального зенитного расстояния Z обратно Н. Так, для светила С₃ Z == 55° N.

Дата добавления: 2014-11-06