
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ая и 2ая экваториальная сис-ма координат
|
|
|
|
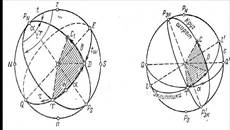
Первая экваториальная система координат. Основным направлением в этой системе является ось мира PnPs, а основными кругами — экватор и меридиан наблюдателя. Положение точки на сфере определяется двумя координатами: склонением и часовым углом (рис. 5).
Склонением δ светила называется дуга меридиана светила от небесного экватора до места светила. Угол δ при центре сферы, равный этой дуге, также называют склонением (его измеряют в обсерваториях). Склонения считаются от 0 до 90° к N или S, например на рис. 5 для светил С1 и С2 имеем 61 = 33° N, б2 = 26° S.
Примечание. В мореходной астрономии принято склонению придавать знак «-+-», если оно одноименно с широтой, и знак «—», если разноименно. В обсерваторной и геодезической астрономии, а также в электронных цифровых вычислительных машинах (ЭЦВМ) знак «+» придается северному склонению (и широте), знак «—» — южному.
Часовым углом t называется дуга экватора от полуденной части меридиана наблюдателя до меридиана светила, считаемая в сторону точки W от О до 360°. В таком счете часовой угол называют вестовым или обыкновенным и наименования обычно не приписывают. Кроме этого, применяется полу круговой счет часовых углов: от 0 до 180° к W или Ost-y, который называют иногда практическим, так как он применяется при решении треугольников и в таблицах. Из рис. 5 видно, что tQst = 360° — tw при tw > 180°. Для светила С1 имеем t = 245° W или t — 115° О1. Дуга экватора ED измеряет центральный угол t или сферический угол при полюсе t, которые также называют часовыми углами.
 Место светила С1 на сфере запишется теперь так: t = 245°; δ = 33° N. Одна экваториальная координата определяет на сфере положение одного круга: часовой угол — положение меридиана светила; склонение — параллели.
Место светила С1 на сфере запишется теперь так: t = 245°; δ = 33° N. Одна экваториальная координата определяет на сфере положение одного круга: часовой угол — положение меридиана светила; склонение — параллели.
Полярные координаты. Положение точки можно определить при полюсе мира — в полярных координатах t и Д. Часовой угол / определяется как угол при повышенном полюсе в полукруговом счете (на рис. 5 t = 115° Ost).
Полярным расстоянием ∆ называется дуга меридиана светила от повышенного полюса до места светила, считаемая от 0 до 180°, например для светила С1 ∆ = 57°, С2 ∆ = 116°. Очевидно, что ∆ = 90° — б. По определению часовой угол отсчитывается от плоскости географического меридиана места, поэтому на рис. 5 и аналогичных всегда изображается местный часовой угол. Для других меридианов часовые углы другие.
Вторая экваториальная система координат. В этой системе при той же оси мира основными кругами являются небесный экватор и меридиан точки Овна (γ). Точка Овна, или точка весеннего равноденствия, расположена в пересечении экватора с эклиптикой, т. е. связана с орбитой Земли. Положение светила в этой системе определяется склонением и прямым восхождением (рис. 6). Склонение б в этой системе аналогично первой экваториальной системе.
Прямым восхождением а светила называется дуга экватора от точки Овна до меридиана светила, считаемая в сторону, обратную W-м часовым углам (т. е. в сторону Ost) от 0 до 360°. Дуге а соответствуют при центре сферы и при полюсе углы а, также называемые прямым восхождением. Например, для светила С1 а =95°; б = 35° N. Вместо α в современных морских пособиях применяется звездное дополнение: т = 360° — а.
Звездным дополнением τ называют дугу экватора от точки Овна до меридиана светила, но считаемую в сторону W-x часовых углов, например для светила С1 имеем τ = 265°. В отечественных пособиях τ применяется только для звезд, отсюда и его название. Направление счета а — прямого восхождения — совпадает с вращением Земли и ее обращением по орбите, отсюда и название координаты.
Полярные координаты. В этом случае прямое восхождение (или τ) считается как угол при полюсе между меридианами точки Овна и светила, а полярное расстояние ∆ аналогично первой системе координат (см. рис. 6). Эта система координат аналогична географическим: а — с λ; б — с φ.
Первая и вторая экваториальные системы отличаются только положением начального меридиана t считается от точки Е, а α— от точки Овна tr, положение же точки Овна определяется ее часовым углом tγw, поэтому (рис. 6) имеем tγ = t + α, (2)
т. е. часовой угол точки Овна (звездное время) равен сумме часового угла и прямого восхождения светила. По этой формуле (в § 23 она названа основной формулой времени) можно перейти от одной системы к другой.
№3 Параллактический треугольник.
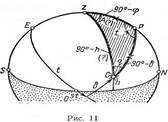
Построив сферу для наблюдателя в данной широте и проведя меридиан и вертикал светила С, получим сферический треугольник PzC, в который входят координаты основных систем и географические координаты места (рис. 11).
Параллактическим треугольником светила называется сферический треугольник PzC, имеющий вершины в повышенном полюсе, зените и месте светила и связывающий между собой основные системы сферических координат. Напомним, что в северной широте повышенный полюс — РN, в южной— PS. Элементами этого треугольника, т. е. его сторонами и углами, являются: сторона zP — дуга меридиана наблюдателя, равная 90° — φ; сторона PC —-дуга меридиана светила, равная 90° — δ; сторона zC — дуга вертикала светила, равная 90°— h; угол при зените, равный азимуту светила в полукруговом счете; угол при повышенном полюсе, равный часовому углу в практическом (полукруговом) счете; угол при светиле q — параллактический угол, также в полукруговом счете. Как видим, в треугольник входят полярные координаты, поэтому его иногда называют полярным треугольником светила.
Формулы, связывающие три данных элемента и один искомый элемент сферического треугольника, называются основными (см. приложение 2). В них углы и стороны должны быть меньше 180°*. В параллактическом треугольнике это достигается использованием полукругового счета t, А и q, стороны же всегда меньше 180°. Следовательно, параллактический треугольник можно решать по основным формулам сферической тригонометрии.
Особое значение параллактического треугольника, отличающее его от других, заключается в том, что он связывает сферические координаты светила с географическими координатами места наблюдателя. Широта входит в сторону zP, а долгота — в угол t; это всегда местный часовой угол tм, а по формуле (3) tм = tгр — λw Поэтому, решая параллактический треугольник, по известным координатам светил можно определить координаты места.
Решение параллактического треугольника по основным формулам. Для решения или для построения треугольника РгС должны быть известны три его элемента. Тогда по основным формулам можно определить остальные его элементы в общем виде, а затем с помощью таблиц функций вычислить эти элементы с нужной точностью.
Треугольник может быть косоугольным при произвольном значении его элементов, прямоугольным, если один или несколько его углов прямые, или четвертным при стороне, равной 90°. Во всех случаях будут справедливы основные формулы, хотя есть и частные формулы и правила для каждого случая. Рекомендуется применять четыре основные формулы сферической тригонометрии, которые следует знать наизусть (см. приложение 2); нужно выучить также формулу пяти элементов,ПРИМЕН В ВЫВОДАХ.
Общий порядок решения параллактического треугольника следующий:
сделать чертеж треугольника, пометить данные и искомые величины;
подобрать формулы для получения искомых величин, как правило, через данные и привести их к простейшему виду;
исследовать формулы на знаки функций (по тригонометрическим четвертям) при данных значениях аргументов; составить простейшие схемы вычислений;
произвести вычисления по таблицам логарифмов или натуральных значений тригонометрических функций;
приписать искомым наименования; произвести контроль вычислений.
Переход от экваториальных координат к горизонтным. Положим, что в треугольнике zPC (см. рис. 11) заданы φ, б и t, требуется определить высоту и азимут. Отметим в параллактическом треугольнике заданные элементы крестиком (X), а искомые — знаком вопроса (?).
Для получения h применим формулу, связывающую три стороны и угол треугольника, т. е. формулу косинуса стороны (см. приложение 2) к стороне zC:
cos (90° — h) == cos (90° —φ) cos (909 — δ) + sin (90Q —φ)sin (90Q —6) cos t. После упрощений получим
sin h = sin φ sin б - cos φ cos δ cos t.
Для получения азимута через заданные величины φ, S, t применим формулу для четырех рядом лежащих элементов,
т. е. формулу котангенсов (см. приложение 2), к углу А:
ctg A sin t = ctg (90° — 6)sin (90° — φ) — cos t cos (90Q — φ), или после упрощений и отделения неизвестного получим
ctg A = tg б cos φ cosec t — sin φ ctg t.
Исследование формул на знаки. Исследование производится определением знака тригонометрической функции при данной величине и знаке координаты с последующим перемножением знаков. Исследование выполняется, чтобы определить: будет ли в правой части двучленной формулы сумма членов (т. е. +1 + II; —I — II) или их разность (например, —I + II); знак искомой функции, а по нему тригонометрическую четверть или знак искомой координаты.
Правила исследования формул на знаки:
1. Широта всегда меньше 90° и считается положительной независимо от наименования (N или S), поэтому все ее функции имеют знак «+»
2. Склонение всегда меньше 90°, но может иметь знак «+», если оно одноименно с φ, и знак «—», если разноименно с φ (знак «—» означает четвертую тригонометрическую четверть). Если б одноименно с φ, все функции б имеют знак «+»; если же б разноименно с φ, то cos б и sec б имеют знак «+». остальные функции — знак «—».
3. Высота всегда меньше 90°, но может иметь знак «+» или «—». Если знак высоты «+», то все ее функции положительны, если же знак «—», то cos h и sec h имеют знак «+»; остальные функции — «—».
4. Часовой угол вводится в треугольник всегда меньшим 180° (Ost или W). Если t<Z 90°, т. е. в первой тригонометрической четверти, то все его функции имеют знак «+». Если же t > 90°, т. е. во второй четверти, то
sin t и cosec t имеют знак «+», остальные функции— «—».
5. Азимут в треугольнике всегда в полукруговом счете, т. е. А может быть в первой и второй четвертях. Поэтому независимо от его наименования, если А < 90°, все его функции имеют знак «+»; если же А > 90°, то sin A и cosec А имеют знак «+», остальные функции — «—».
6. Параллактический угол имеет величину от 0 до 180°, и знаки его функций определяются аналогично А и t.
Эти же правила применяются и при определении знака или величины искомой координаты.
Треугольники со сторонами, меньшими 180°, называются эйлеровыми. Возможны сферические треугольники с элементами от 0 до 360° (Мебиуса). В них при тех же формулах правила счета и знаков другие
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 940; Нарушение авторских прав?; Мы поможем в написании вашей работы!