Определение широты по Солнцу и по Полярной

Теория метода.

Высота полюса мира над горизонтом всегда равна широте места. К сожалению, в самих полюсах нет звезд, измеряя высоты которых, можно было практически сразу после исправления поправками получать широту. Но недалеко от северного полюса РN находится достаточно яркая звезда α Малой Медведицы, называемой Полярной звездой. Координаты Полярной на 2001 г. α = 38°45' и δ= 89°16'. Следовательно, её полярное расстояние Δ = 90° -δ < 1° = 44'. Поэтому высота Полярной звезды близка к широте и может отличаться на небольшую величину х.

Пусть Полярная звезда находится в произвольной точке С. Из данной точки опустим сферический перпендекуляр на меридиан наблюдателя. Величина х - есть проекция полрного расстояния на меридиан наблюдателя. Так как полярное расстояние мало (44'), то прямоугольный треугольник PNCD можно считать плоским.

Из данного прямоугольного треугольника имеем x = Δcostм

Из рисунка видно, что φ= ho - x (*)

На основании основной формулы времени, имеем x =Δ сos(Sм -α).

Подставляя в формулу (*) значение х, получаем φ= ho - Δсos(Sм - α)

Ведём обозначения I =Δ - o сos(Sм -α o) (**)

αo и Δo - среднегодовые значения прямого восхождения и полярного расстояния Полярной звезды.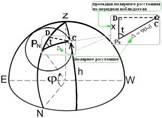

Окончательно широта по высоте Полярной звезды определяется следующей формулой   φ = ho + I + II + III (4.8) Поправка I учитывает суточное вращение Полярной звезды вокруг северного полюса мира, как видно из формулы (**) зависит только от звездного времени и выбирается из МАЕ из таблицы "Широта по высоте Полярной звезды" на страницах 277-278.   Поправка II учитывает сферичнось треугольника PNCD и корректирует поправку I, всегда положительная, выбирается из МАЕ из таблицы "Широта по высоте Полярной звезды" на странице 279 по аргументам Sм и h.   Поправка III учитывает изменение в течении года экваториальных координат Полярной звезды корректирует поправку I выбирается из МАЕ из таблицы "Широта по высоте Полярной звезды" на странице 280 по аргументам Sм и дата.   И так как все поправки зависят от звездного местного времени, следовательно, для определеня широты по высоте Полярной звезды кроме исправления высот необходимо расчитать звездное местное время, чтобы по этому аргументу выбрать поправки I, II и III Достоинства и недостатки метода. Рассчитывав широту, её можно использовать, как высотную ЛП, которая будет проходить по параллели. Наблюдения Полярной звезды происходят с наблюдения других звезд, для которых элементы ВЛП рассчитываются традиционным образом. На Полярной звезде судоводители экономят до 40% времени вычислений - в этом и заключается преимущества использования Полярной звезды для ОМС по нескольким звездам.   К недостатку данного метода можно отнести его ограниченность по широте. Его можно использовать только в северном полушарии (наиболее благоприятный диапазон широт 5°N < < 65°N). В южном полушарии вблизи южного полюса нет яркой приполярной звезды. Определение широты по меридиональной высоте светила. Если светило находится на меридине наблюдателя (чаще всего это происходит в момент верхней кульминации), то его высота является меридиональной H. В этом случае легко получить широту. Напоминаем, что высота h наименование не имеет. Но если светило находится на меридиане наблюдателя, то меридиональная высота H одноименно с точкой (N или S), над которой измеряется высота. В этом же случае зенитное расстояние Z = 90 - H разноименно с H. Рассмотрим на следующем рисунке несколько вариантов кульминации светила и выведем формулу для нахождения широты.

Учёт движения судна

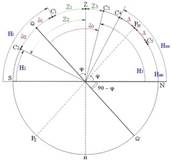С1:δ<φ-- одноименны, HS-меридиональная высота,ZN-зенитное расстояние φN = ZN +δ N   C2, разноименны,HS,ZN φN = ZN – δS   C3,δ>φ одноименны, HN,ZN, φN =δN – ZS   C4 одноименны, но δ> 90 – φ.Светило незаходящее Hвк-верхняя кульминация φN = Hвк –Δ   C5 одноименны,но δ > 90 – φ Hнк-нижняя кульминация φN = Hнк + Δ Светило незаходящее   Напоминаем, что Δ= 90 - φ - это полярное расстояние, это расстояние от полюса до светила. Объединяя варианты для светил С1 - С3, в общем виде получаем следующую формулу:   φ = Z ± δ (4.7) т.е., если Z и δ одноименны, то знак +, если же Z и δ разноименны, то знак -, причем вычитаем из большей величины меньшую и широте приписываем знак наибольшей величины. Если в качестве светила С использовать Солнце, то вариант светила С3 возможен только в тропиках, а вариант светил С4 и С5 возможен тоько за полярным кругом. Достоинства и недостатки метода. Простота и малый объём вычислений. Для Солнца этот метод можно использовать только один раз в сутки (кроме полярных широт). Неблагоприятные гидрометеоусловия в момент кульминации не позволяют применить данный способ.

Данным способом можно определить только одну координату - широту.

Дата добавления: 2014-11-06