Линейно-взвешенное скользящее среднее (Linear Weighted Moving Average, LWMA)

Сглаженное скользящее среднее (Smoothed Moving Average, SMMA)

Экспоненциальное скользящее среднее (Exponential Moving Average, EMA)

Простое скользящее среднее (Simple Moving Average, SMA)

Расчет

Простое, или арифметическое, скользящее среднее рассчитывается путем суммирования цен закрытия инструмента за определенное число единичных периодов (напр., 12 часов) с последующим делением суммы на число периодов.

SMA = SUM (CLOSE (i), N) / N

Где:
SUM — сумма;
CLOSE (i) — цена закрытия текущего периода;
N — число периодов расчета.

Экспоненциально сглаженное скользящее среднее определяется путем добавления к предыдущему значению скользящего среднего определенной доли текущей цены закрытия. В случае экспоненциальных скользящих средних больший вес имеют последние цены закрытия. Р-процентное экспоненциальное скользящее среднее будет иметь вид:

EMA = (CLOSE (i) * P) + (EMA (i - 1) * (100 - P))

Где:
CLOSE (i) — цена закрытия текущего периода;
EMA (i - 1) — значение скользящего среднего предыдущего периода;
P — доля использования значения цен.

Первое значение этой сглаженной рассчитывается, как и простая скользящая средняя (SMA).

SUM1 = SUM (CLOSE (i), N)
SMMA1 = SUM1 / N

Второе и последующие скользящие средние рассчитываются по следующей формуле:

SMMA (i) = (SUM1 - SMMA (i - 1) + CLOSE (i)) / N

Где:
SUM — сумма;
SUM1 — сумма цен закрытия N периодов, отсчитываемая от предыдущего бара;
SMMA (i - 1) — сглаженное скользящее среднее предыдущего бара;
SMMA (i) — сглаженное скользящее среднее текущего бара (кроме первого);
CLOSE (i) — текущая цена закрытия;
N — период сглаживания.

Во взвешенном скользящем среднем последним данным присваивается больший вес, а более ранним — меньший. Взвешенное скользящее среднее рассчитывается путем умножения каждой из цен закрытия в рассматриваемом ряду на определенный весовой коэффициент.

LWMA = SUM (CLOSE (i) * i, N) / SUM (i, N)

Где:
SUM — сумма;
CLOSE(i) — текущая цена закрытия;
SUM (i, N) — сумма весовых коэффициентов;
N — период сглаживания.

Как недостаток можно отметить систематическое запаздывание сигнала. Достоинство - легко определить направление тренда, также можно использовать их как линии поддержки и сопротивления. Обычно используют две линии средних с разными периодами: одну более быструю с коротким периодом, а другую более медленную с длинным периодом.

Скользящие средние используются только на трендовых рынках. В условиях бокового тренда ценность сигналов подаваемых ими низкая из-за сильного запаздывания.

Рекомендуемые порядки средней:

График цен	Порядки средней
недельный	8, 13, 21
дневной	8, 13, 21, 55, 89
4-часовой	8, 34, 55, 89, 144
1-часовой	5, 13, 21,34, 55, 89, 144
менее 15 минут	34, 55, 144

(Moving) Индикатор сильно запаздывает! Но он очень хорошо показывает направление тренда! Следовательно, используем его для выявления направления тренда.

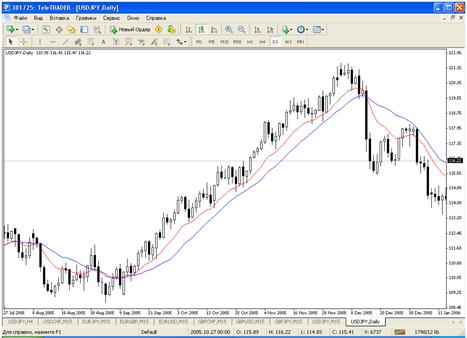
Дата добавления: 2014-11-06