Уравнение линии на плоскости. Точка пересечения двух линий

Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерии знакоопределенности квадратичной формы (через собственные значения ее матрицы и по критерию Сильвестра)

Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм

Определение 1. Квадратичная форма L (x ₁, x ₂, …, x _n) от n переменных называется канонической, если все её коэффициенты при произведениях различных переменных равны нулю, т.е. a _ij=0 при i ¹ j.

В этом случае квадратичная форма имеет вид .

Доказано, что любая квадратичная форма с помощью линейного невырожденного преобразования может быть приведена к каноническому виду.

При этом её матрица приводится к диагональному виду.

Теорема 1 (закон инерции квадратичных форм). Ранг квадратичной формы не меняется при линейных преобразованиях.

Следовательно, ранг квадратичной формы L (x ₁, x ₂, …, x _n) от n переменных равен числу отличных от нуля коэффициентов канонической формы и совпадает с рангом соответствующей диагональной матрицы.

Определение 1. Квадратичная форманазывается положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля, выполняется неравенство

L (x ₁, x ₂, …, x _n)>0 (L (x ₁, x ₂, …, x _n)<0).

Теорема 1 ( критерий определенности квадратичной формы). Для того чтобы квадратичная форма L = X¢AX была положительно (отрицательно) определена, необходимо и достаточно, чтобы все собственные значенияl_i матрицы A были положительны (отрицательны).

Теорема 2 ( критерий Сильвестра). Для того чтобы квадратичная форма L = X¢AX была положительно определена, необходимо и достаточно, чтобы все главные миноры матрицы A были бы положительны, т.е.

, , …, .

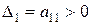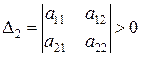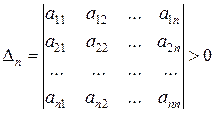Для того чтобы квадратичная форма L = X¢AX была отрицательно определена, необходимо и достаточно, чтобы знаки главных миноров матрицы A чередовались, начиная со знака «минус» для минора первого порядка, т.е.

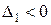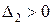, , и т.д.

Тема 6: Элементы аналитической геометрии

Дата добавления: 2014-11-06