Рішення

Задача планування виробництва

Підприємство випускає 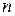виробів. Для їх виробництва необхідно 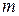ресурсів (сировини, матеріалів, робочого часу, грошей, машинного часу і т. п.).

Початкові дані наведені в табл. 1.1.

Таблиця 1.1

Вид ресурсу	Технологічні норми витрат i -го ресурсу на j -й виріб	Запас ресурсу
		...		...
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
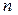
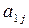
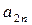
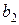
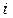
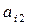
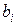
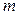
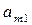
Прибуток від одного виробу			...		...
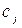
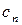
Кількість виробів			...		...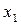

У таблиці позначено:

– технологічні коефіцієнти (які визначають норми витрат i -го ресурсу на j -й виріб); 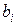– запас i -го ресурсу; – ефективність j -го виробу (наприклад, прибуток). Ці показники вважаються постійними, тобто .

– кількість j -го виробу .

Завдання: скласти такий план випуску виробів 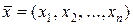, щоб отримати максимальну ефективність (максимальний прибуток).

Математичний опис задачі складається з функції мети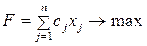

та обмежень:

Побудувати математичну модель задачі.

Задача 1.1. Підприємство, використовуючи три види ресурсів S ₁, S ₂ і S ₃, виробляє продукцію чотирьох видів P ₁, P ₂, P ₃ і P ₄. Запаси ресурсів, число одиниць ресурсів, необхідних на виробництво одиниці кожного виду продукції, а також прибуток від реалізації одиниці кожного виду продукції, наведені в табл. 1.2.

Таблиця 1.2

Вид ресурсу	Число одиниць ресурсів, необхідних на виробництво одиниці продукції, умовн. од.	Запас ресурсу, умовн. од.
P 1	P 2	P 3	P 4
S 1
S 2
S 3
Прибуток від од. продукції, грн

Визначити план випуску продукції, що забезпечить максимальний прибуток.

Побудуємо математичну модель задачі.

Позначимо через х_j – кількість одиниць продукції j- го виду (j =1, 2, 3, 4), запланованих до виробництва. Для їх виготовлення необхідно х ₁+2 х ₂+ х ₃ одиниць ресурсу S ₁, х ₁+ х ₂+2 х ₃+ х ₄ одиниць ресурсу S ₂ і х ₁+3 х ₂+3 х ₃+2 х ₄ одиниць ресурсу S ₃. Споживання ресурсів S ₁, S ₂ і S ₃ не має перевищувати їх запасів, відповідно 18, 30 та 40 одиниць, тому зв'язок між споживанням ресурсів та їхніми запасами задається системою нерівностей:

(1.1)

Кількість одиниць продукції не може бути від’ємною, тому

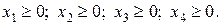(1.2)

Сумарний прибуток f складе грн від реалізації продукції P ₁, грн – від реалізації продукції P ₂, грн – від реалізації продукції P ₃ і 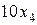грн – від реалізації продукції P ₄, тобто

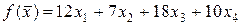. (1.3)

Отже, математична модель задачі планування виробництва: знайти такий план випуску продукції , що задовольнить системі (1.1) і умові невід'ємності (1.2), при якому функція (1.3) набуде максимального значення

1.2. Задача складання раціону (задача про дієту, задача про суміші)

Ще один клас моделей виникає з економічних проблем, пов’язаних з виготовленням різних сумішей:

· у сільськогосподарському виробництві при визначенні складу добрив;

· при використанні різних видів пального для отримання пального іншої марки;

· в металургії при виготовленні сталі з кількох марок сталі;

· при складанні раціону харчування сім’ї, спортсменів, худоби.

Початкові дані наведені в табл. 1.3.

Таблиця 1.3

Вид компонента	Вага i -го компонента (кг) в одному кг j -го матеріалу	Потрібна вага компонента в суміші, кг
		...		...
			...		...
			...		...
...	...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...	...
			...		...
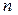
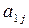
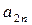
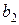
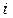
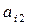
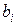
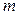
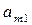
Ціна 1 кг матеріалу, грн/кг			...		...
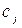
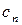
Загальна вага матеріалу в суміші, кг			...		...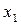

У таблиці позначено:

– вага i -го компонента (кг) в одному кг j -го матеріалу; 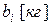– потрібна вага i -го компонента у вихідній суміші; – ціна одного кг j -го матеріалу. Ці показники вважаються постійними, тобто .

– загальна вага j -го матеріалу в суміші .

Завдання: отримати суміш 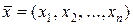мінімальної вартості .

Математичний опис задачі складається з функції мети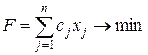

та обмежень: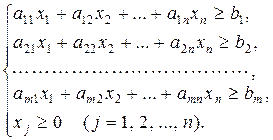

Побудувати математичну модель задачі.

Задача 1.2. До добового раціону сім’ї входять два продукти: м’ясо і фрукти. Щодо кожного з продуктів відомо: скільки в одному кілограмі міститься білка, вітаміну А, вітаміну В, вітаміну С та вартість одного кілограму м’яса та фруктів. Обчислити загальну вагу продуктів у раціоні мінімальної вартості, при умові, що у сукупності всі продукти повинні містити не менше заданої кількості компонентів (білка, вітаміну А, вітаміну В, вітаміну С).

Таблиця 1.4

Вид компонента	Вага компонента (у. о.) в одному кг продукту	Потрібна вага компонента в раціоні, у. о.
Продукт №1	Продукт №2
Білок		0,9
Вітамін А	0,09
Вітамін В	4,1	-
Вітамін С	-	7,1
Ціна 1 кг продукту, грн/кг

Дата добавления: 2014-11-06