Рішення. Побудуємо математичну модель задачі

Транспортна задача

Рішення

Побудуємо математичну модель задачі.

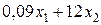Позначимо через х_j – загальну вагу продукту j- го виду (j =1, 2) в раціоні. Тоді цей раціон буде містити одиниць білка, одиниць вітаміну А, 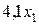одиниць вітаміну В і одиниць вітаміну С. Оскільки ці кількості поживних речовин в раціоні не можуть бути менше заданих границь, відповідно 10, 4, 1 і 1, то маємо систему нерівностей:

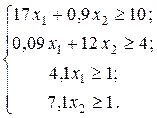(1.4)

Загальна вартість раціону

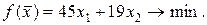(1.5)

Таким чином, математична модель задачі складання раціону така: скласти добовий раціон 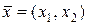, що задовольнить системі (1.4), при якому функція (1.5) набуде мінімального значення.

Маємо 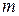постачальників і 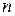споживачів. Початкові дані наведені в таблиці постачань (табл. 1.5).

Таблиця 1.5

Запаси постачальників	Потреби споживачів
		...		...
			...		...
			...		...
...	...	...	...	...	...	...
			...		...
...	...	...	...	...	...	...
			...		...

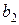
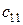
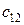
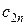
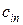
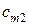
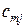
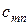
У таблиці позначено:

– запас товару у i -го постачальника; – потреби у товарі j -го споживача; – витрати на транспортування одиниці товару від i- го постачальника j- му споживачу. Ці показники вважаються постійними, тобто .

Завдання: знайти план перевезень для задоволення потреб, за яким загальні витрати були б мінімальними.

Для побудови математичної моделі даної задачі позначимо через 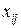обсяг товару, який необхідно перевезти від i- го постачальника j- му споживачу . Оскільки обсяг товару не може бути від’ємним, маємо обмеження: .

План перевезень задається матрицею , а загальні витрати – функцією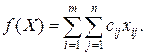

Можливі три ситуації.

1. Попит дорівнює пропозиції: .

Математичний опис задачі складається з функції мети

та обмежень: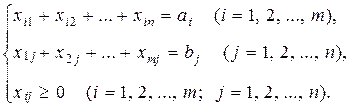

В даній ситуації в системі обмежень перші m рівнянь описують обмеження для постачальників (все, що вивезено від i -го постачальника всім споживачам, точно дорівнює його запасу), наступні n рівнянь – обмеження для споживачів (все, що ввезено j -му споживачу від усіх постачальників, точно дорівнює його потребі), останні – умову невід’ємності змінних.

Така транспортна задача вважається замкненою, всі інші – відкритими.

2. Попит менший за пропозицію: .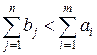

Математичний опис задачі складається з функції мети

та обмежень:

В даній ситуації в системі обмежень перші m рівнянь описують обмеження для постачальників (все, що вивезено від i -го постачальника всім споживачам, не перевищує його запасу), наступні n рівнянь – обмеження для споживачів (все, що ввезено j -му споживачу від усіх постачальників, точно дорівнює його потребі).

3. Попит більший за пропозицію: .

Математичний опис задачі складається з функції мети

та обмежень:

В даній ситуації все, що вивезено від i -го постачальника всім споживачам, точно дорівнює його запасу, а все, що ввезено j -му споживачу від усіх постачальників, не перевищує його потреби.

Побудувати математичну модель задачі.

Задача 1.3. Вихідні дані транспортної задачі подані у вигляді таблиці постачань (табл. 1.6).

Таблиця 1.6

	bj
ai

Необхідно знайти обсяги перевезень, за якими загальні витрати були б мінімальними.

Побудуємо математичну модель транспортної задачі.

Позначимо 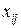– обсяг товару, який необхідно перевезти від i- го постачальника j- му споживачу , тоді план перевезень задається матрицею .

Сумарний обсяг товару, який є у постачальників, дорівнює

.

Сумарний обсяг товару, потрібного споживачам, дорівнює

.

У даній задачі попит більший за пропозицію, тобто 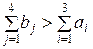, тому увесь товар, що є у кожного з постачальників, буде вивезений, але потреби в товарі деяких споживачів не будуть цілком задовільнені.

Отже, математична модель транспортної задачі така:

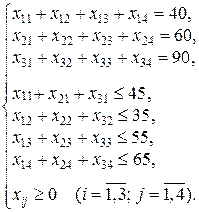
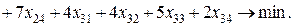
1.4. Задача про мінімізацію відходів

Модель задачі про раціональний розкрій матеріалів має важливе значення для економії матеріалів і сировини. Розглянемо постановку задачі.

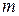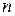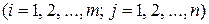На розкрій надходить матеріал у вигляді певних одиниць стандартних розмірів. Потрібно з нього виготовити різних виробів. Задано асортимент цих виробів, тобто – відповідно нижня і верхня границі кількості виробів i -го виду. Кожна одиниця вихідного матеріалу може бути розкроєна різними способами, причому використання j -го способу дає одиниць i -го виробу . Відома величина відходів з одиниці стандартного матеріалу при j -му способі розкрою.

Необхідно знайти план розкрою, що забезпечує заданий асортимент виробів при мінімальних сумарних відходах матеріалів.

За невідому беремо число одиниць вихідного матеріалу, що потрібно розкроїти j -v способом, тоді 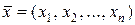– план розкрою. Через 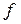позначимо загальну кількість відходів. Кількість заготовок i -го виду запишемо у вигляді .

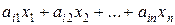Тоді математична модель задачі має вигляд:

.

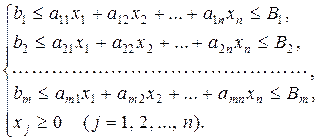
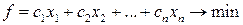Характер моделі може змінитися, якщо в умові задати іншу мету. Наприклад, якщо ставиться задача про одержання заданої кількості виробів з найменшою кількістю вихідного матеріалу, то функція мети має вигляд:

Побудувати математичну модель задачі.

Задача 1.4. Рулони лінолеуму довжиною 30 м треба розрізати на шматки довжиною 15, 10 та 6 м. Причому шматків по 15 м необхідно не більш 20, шматків по 10 м – не менш 16, а шматків по 6 м – не менше 12 та не більше 22. Визначити оптимальний план розкрою лінолеуму з точки зору мінімізації відходів.

Дата добавления: 2014-11-06