Электродинамические силы между параллельными проводниками

Возьмем два параллельных круглых проводника 1 и 2 (рис. 2-1, в), расположенных в одной плоскости на расстоянии а друг от друга и обтекаемых токами i ₁ и i ₂. Расчет будем производить первым методом. Проделав все операции аналогично (2-2) – (2-8) и учитывая, что sin β = 1, так как проводники расположены в одной плоскости, и вектор индукции в данном случае перпендикулярен этой плоскости (β = 90°), получим

, (2-15)

где

.

Выразим подынтегральные переменные второго интеграла через одну из переменных, а именно через угол α. Примем за начало координат элемент dy и направление токов, совпадающее с положительным направлением координат. В этом случае текущая координата

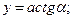
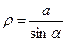; (2-16)

Подставив полученные выражения в (2-15) и считая, что проводник 2 распространяется от – ∞ до + ∞, чему соответствует изменение угла α от π до 0, получим

(2-17)

Очевидно, если проводник l (l₁), так же как и проводник 2, распространяется до ± ∞, то с будет стремиться к бесконечности. Если проводник l имеет конечную длину, то

(2-18)

Согласно (2-8) сила, действующая на проводник l, равна

(2-19)

Уравнение (2-19) Определяет силу взаимодействия между двумя проводниками, один из которых бесконечно длинен, а второй имеет конечную длину l и расположен симметрично относительно первого. В случае когда оба проводника будут иметь конечную длину l, пределы интегрирования для (2-17) будут уже не от π до 0, а от α₂ до α₁ (см. штриховые линии на рис. 2-1, в) и сила взаимодействия между двумя круглыми проводниками конечной и равной длины определится уравнением

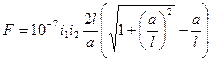. (2-20)

В (2-20) множитель перед скобкой представляет собой силу взаимодействия между двумя проводниками, один из которых имеет бесконечную длину. Обозначим эту силу через F_∞. Коэффициент, заключенный в скобках, представляет собой величину, меньшую единицы. При а / l < 0,2 (в практике, как правило, а / l < 0,2) величиной (а / l)² по отношению к единице можно пренебречь. Тогда уравнение (2-20) примет вид

В практике весьма часто проводники имеют неравную длину. Силу взаимодействия между такими проводниками можно найти изложенным выше способом, произведя интегрирование каждый раз в соответствующих пределах. Можно эту задачу решить, применив уравнение (2-20).

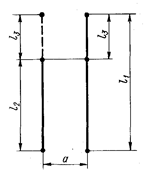
Рис. 2-2. К определению электродинамической силы между параллельными проводниками неравной длины

На рис. 2-2 приведены два проводника неравной длины l ₁ и l ₂, расположенные друг от друга на расстоянии α и обтекаемые токами i ₁ и i ₂; Нарастим проводник l ₂ на отрезок l ₃ до длины, равной l ₁. Проводник l ₁ можем также представить состоящим из двух отрезков l ₂ и l ₃. Тогда можем написать, что сила взаимодействия между проводниками длиной l ₁ и l ₂ (F 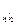) равна сумме сил взаимодействия между двумя проводниками l ₂ одинаковой длины (F 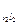) и двумя проводниками длиной l ₂ и l ₁, (F ):

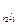Аналогично можно написать

Сложив уравнения (2-22) и (2-23), получим

Таким образом, сила взаимодействия между двумя проводниками неравной длины выражается через силу взаимодействия проводников равной длины:

При этом l ₁ и l ₂ – величины заданные, а l ₃ = l ₁ – l ₂.

Сила взаимодействия между параллельными круглыми проводниками может быть также определена по изменению запаса электромагнитной энергии.

Первый случай – оба проводника принадлежат к одной системе. Индуктивность системы из двух параллельных проводников радиусом r и длиной l, находящихся на расстоянии а, при условии, что l >> а, определяется формулой [24]

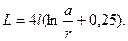(2-26)

Нас интересует сила, действующая в направлении а. Согласно (2-13)

(2-27)

из (2-26)

тогда

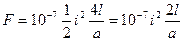(2-28)

Из (2-28) видно, что результат получился таким же, как при определении этих сил первым методом.

Второй случай – проводники принадлежат к двум различным системам, при этом сами системы не претерпевают деформации. Взаимная индуктивность между двумя проводниками длиной;, находящимися друг от друга на расстоянии а. пои условии, что l >> а. определяется формулой

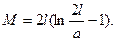(2-29)

Согласно (2-14) сила, действующая в направлении а,

,

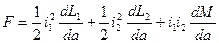здесь

; ,

так как сами системы не претерпевают деформации, а из (2-29)

Тогда

(2-30)

т.е. результат, как и следовало ожидать, получился тот же.

Для двух параллельных проводников, расположенных с любым сдвигом, Г. Б. Холявский [31]. получил удобную для расчетов коэффициента контура формулу, основанную на геометрической интерпретации приведенных выше уравнений.

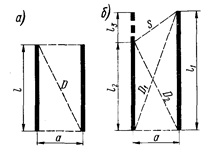
Рис. 2-3. К определению электродинамической силы графическим методом

Величина представляет собой длину диагонали D (рис. 2-3, а) прямоугольника со сторонами ; и а; следовательно, согласно (2-20) для проводников равной длины

(2-31а)

а согласно (2-25) для проводников неравной длины (рис. 2-3, б)

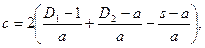(2-31б)

т.е. коэффициент контура равен разности суммарных диагоналей и боковых сторон четырехугольника (прямоугольник, трапеция, параллелограмм), построенного на данных отрезках проводников, деленной на его высоту.

Аналогичную, но более сложную интерпретацию можно получить и для перпендикулярно расположенных проводников.

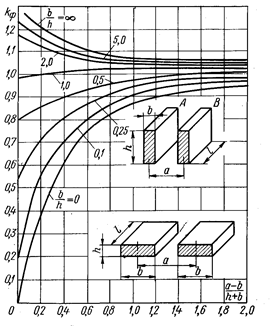
Рис. 2-4. Зависимость коэффициента k _ф от размеров проводников

Приведенные выше уравнения справедливы для проводников круглого и трубчатого сечений, для которых можно считать, что ток протекает по их геометрической оси. Для проводников прямоугольного сечения (шин) следует вводить поправочный коэффициент – коэффициент формы k _ф зависящий от размеров проводников и расстояний между ними (рис. 2-4):

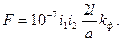(2-32)

Дата добавления: 2014-10-15