Неравномерное кодирование

Кодирование словаря

Сжатие данных

Сжатие возможно, т.к. данные на выходе источника содержат избыточную и/или плохо различимую информацию.

Плохо различимая информация - информация, которая не воздействует на ее приемник. Подобная информация сокращается или удаляется при использовании сжатия с потерями. При этом энтропия исходной информации уменьшается. Сжатие с потерями применяется при сжатии цифровых изображений и оцифрованного звука.

Приемы, применяемые в алгоритмах сжатия с потерями:

- использование модели – подбор параметров модели и передача только одних параметров;

- предсказание – предсказание последующего элемента и передача величины ошибки;

- дифференциальное кодирование – передача изменений последующего элемента при сравнении с предыдущим.

Избыточная информация – информация, которая не добавляет знаний о предмете. Избыточность может быть уменьшена или устранена с помощью сжатия без потерь (эффективного кодирования). При этом энтропия данных остается неизменной. Сжатие без потерь применяется в системах передачи данных.

Приемы, применяемые в алгоритмах сжатия без потерь:

- кодирование длин последовательностей – передача числа повторяющихся элементов;

- кодирование словаря – использование ссылок на переданные ранее последовательности, а не их повторение;

- неравномерное кодирование – более вероятным символам присваиваются более короткие кодовые слова.

Позволяет уменьшить избыточность, вызванную зависимостью между символами. Идея кодирования словаря состоит в замене часто встречающихся последовательностей символов ссылками на образцы, хранящиеся в специально создаваемой таблице (словаре). Данный подход основан на алгоритме LZ, описанном в работах израильских исследователей Зива и Лемпеля.

Позволяет уменьшить избыточность, вызванную неравной вероятностью символов. Идея неравномерного кодирования состоит в использовании коротких кодовых слов для часто встречающихся символов и длинных – для редко возникающих. Данный подход основан на алгоритмах Шеннона-Фано и Хаффмана.

Коды Шеннона-Фано и Хаффмана являются префиксными. Префиксный код – код, обладающий тем свойством, что никакое более короткое слово не является началом (префиксом) другого более длинного слова. Такой код всегда однозначно декодируем. Обратное неверно.

Код Шеннона-Фано строится следующим образом. Символы источника выписываются в порядке убывания вероятностей (частот) их появления. Затем эти символы разбиваются на две части, верхнюю и нижнюю, так, чтобы суммарные вероятности этих частей были по возможности одинаковыми. Для символов верхней части в качестве первого символа кодового слова используется 1, а нижней – 0. Затем каждая из этих частей делится еще раз пополам и записывается второй символ кодового слова. Процесс повторяется до тех пор, пока в каждой из полученных частей не останется по одному символу.

Пример1.1:

Таблица 1.1 – Построение кода Шеннона-Фано.

Символ	Вероятность	Этапы разбиения	Код
а1 а2 а3 а4 а5	0,40 0,35 0,10 0,10 0,05

Алгоритм Шеннона-Фано не всегда приводит к построению однозначного кода с наименьшей средней длиной кодового слова. От отмеченных недостатков свободен алгоритм Хаффмана.

Код Хаффмана строится следующим образом. Символы источника располагают в порядке убывания вероятностей (частот) их появления. Два самых последних символа объединяют в один вспомогательный, которому приписывают суммарную вероятность. Полученные символы вновь располагают в порядке убывания вероятностей, а два последних объединяют. Процесс продолжается до тех пор, пока не останется единственный вспомогательный символ с вероятностью 1. Для нахождения кодовых комбинаций строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви. Ветви с большей вероятностью присваивается символ 1, с меньшей – 0. Такое ветвление продолжается до достижения вероятности каждого символа. Двигаясь по кодовому дереву сверху вниз, записывают для каждого символа кодовую комбинацию.

Пример1.2:

Таблица 1.2 – Построение кода Хаффмана.

Символ	Вероятность	Объединение символов	Код
а1 а2 а3 а4 а5	0,40 0,35 0,10 0,10 0,05	0,40 0,35 0,15 0,10	0,40 0,35 0,25	0,60 0,40	1,00

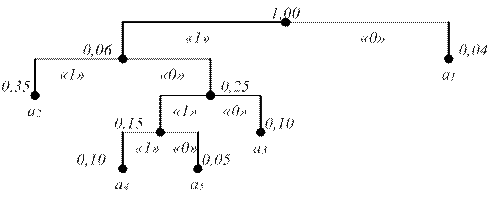
Рисунок 1.2 – Кодовое дерево для кода Хаффмана.

Домашнее задание:

1. [3.1.2] с.13…16;

[3.1.3] с.174…176;

[3.1.5] с. 109…112, 131…135, 297…299;

[3.1.14] с. 146…155;

[3.1.15] с.11…14.

2. Файл состоит из некоторой символьной строки:

«aaaaaaaaaabbbbbbbbccccccdddddeeeefff».

Закодировать символы кодами Шеннона-Фано и Хаффмана и оценить достигнутую степень сжатия.

РЕШЕНИЕ ЗАДАЧИ ДОМАШНЕГО ЗАДАНИЯ:

Рассчитаем частоты появления символов: υ (а)=10/36=0,28; υ (b)=8/36=0,22; υ (c)=6/36=0,17; υ (d)=5/36=0,14; υ (e)=4/36=0,11; υ (f)=0,08.

Таблица 1.3 – Построение кода Шеннона-Фано.

Символ	Частота	Этапы разбиения	Код
a b c d e f	0,28 0,22 0,17 0,14 0,11 0,08

Достигнутая в результате кодирования степень сжатия определяется коэффициентом сжатия:

,

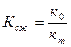где к₀ – первоначальный размер данных;

к_m – размер данных в сжатом виде.

При кодировании кодом Шеннона-Фано обеспечивается коэффициент сжатия:

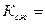36∙¯| log₂ 6|¯/(10∙2+8∙2+6∙3+5∙3+4∙3+3∙3)=108/90=1,2,

где 36 – количество символов в файле;

¯| log₂ 6|¯ - минимальная длина кодовой комбинации при кодировании равномерным кодом (¯|.|¯ обозначает ближайшее целое число, большее log ₂6);

10, 8, 6, 5, 4, 3 – число символов a, b, c, d, e, f в файле;

2, 2, 3, 3, 3, 3 – длина кодовых комбинаций кода Шеннона-Фано, соответствующих символам a, b, c, d, e, f (см. таблицу 1.1).

Таблица 1.3 – Построение кода Хаффмана.

Символ	Частота	Объединение символов	Код
a b c d e f	0,28 0,22 0,17 0,14 0,11 0,08	0,28 0,22 0,19 0,17 1,14	0,31 0,28 0,22 0,19	0,41 0,31 0,28	0,59 0,41	1,00

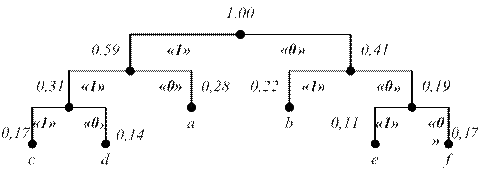
Рисунок 1.3 – Кодовое дерево для кода Хаффмана.

При кодировании кодом Хаффмана обеспечивается степень сжатия:

К_сж =36∙¯| log₂ 6|¯/(10∙2+8∙2+6∙3+5∙3+4∙3+3∙3)=108/90=1,2.

Дата добавления: 2014-11-06