Вопрос 2.2. Основное уравнение центробежного насоса

Согласно известной из курса гидравлики одноразмерной теории движение массы жидкости в рабочем колесе может быть уподоблено движению одной элементарной струйки, т.е. движение всей массы жидкости в рабочем колесе рассматривается как движение одинако­вых элементарных струек в колесе с бесконечно большим числом эле­ментарно тонких лопаток.

При этом, кроме того, допускается, что траектории движения от­дельных частиц жидкости одинаковы с формой лопаток.

Стенки проточных каналов в корпусе центробежного насоса не­подвижны, поэтому скорости потока относительно этих стенок явля­ются абсолютными скоростями.

При движении внутри канала рабочего колеса частица жидкости имеет по отношению к колесу относительную скорость ω, которая на­правлена касательно к лопатке в точке ее приложения. Но благодаря вращению колеса при числе оборотов п частица жидкости приобрета­ет и окружную скорость, направленную касательно к окружности ра­диуса r, определяемую как произведение угловой скорости на радиус r - расстояние рассматриваемой частицы от центра вращения, т. е.:

u= ω·r=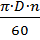

Следовательно, частица жидкости, покидая рабочее колесо, будет иметь окружную скорость по касательной к наружному диаметру ко­леса в точке выхода и относительную скорость, направленную каса­тельно к выходной кромке лопатки. В результате геометрического сложения этих скоростей (и и ω) частица жидкости будет иметь абсо­лютную скорость с по их равнодействующей (по диагонали парал­лелограмма, построенного на направлениях скоростей и и ω), в на­правлении которой элементарные струйки жидкости будут выходить из рабочего колеса (рис. 2.2.).

Угол, образуемый между направлениями абсолютной скорости с и окружной скорости и, обозначают через α. Угол между касательны­ми к лопатке и к окружности в направлении, противоположно направ­лению окружной скорости, обозначают через β. Этот угол определя­ет направление относительной скорости ω.

-42-

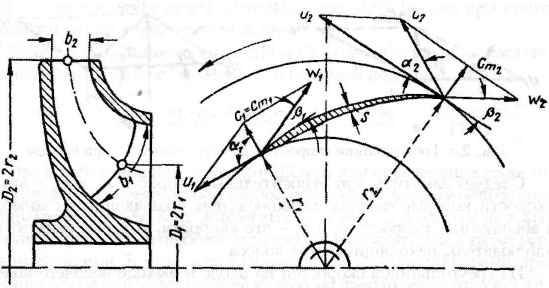
Рис. 2.2. Движение жидкости в каналах рабочего колеса

Абсолютную скорость можно рассматривать как результирующую двух скоростей:

- с_и - совпадающей по направлению с окружной скоростью и являющейся проекцией скорости с на окружную и равной:

с_и = с·

- с_т - меридиональной, направленной по радиусу г и равной:

Для скоростей входа и выхода из колеса обозначения одинаковы, только входным скоростям придается индекс 1, а выходным - индекс 2. Тогда будем иметь:

1) при входе на лопатки

- ω₁ – относительную скорость,

- с₁ – абсолютную скорость,

- и₁ – окружную скорость:

u₁= ;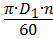

2) при выходе с лопаток

- ω₂ - относительную скорость,

- с₂ - абсолютную скорость,

- и₂ - окружную скорость:

u₂= ,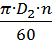

где D₁ - внутренний диаметр рабочего колеса;

D₂ - наружный диаметр рабочего колеса;

п - число оборотов рабочего колеса в минуту.

-43-

Следует заметить, что относительные скорости а>₁ и ох, - это те скорости, которые заметил бы наблюдатель, вращающийся с колесом, а абсолютные скорости с₁ и с₂ - это скорости, которые заметил бы наблюдатель, находящийся вне колеса.

Из треугольников скоростей на входе и выходе рабочего колеса получим следующие зависимости:

(2.1)

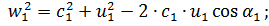(2.2)

Каждый килограмм жидкости, протекающий через колесо, обла­дает кинетической энергией (скоростным напором) 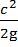и, находясь под давлением р, имеет потенциальную энергию . Если обозна­чить через р₁ и р₂ соответственно давление при входе и выходе из ра­бочего колеса, получим полный напор, развиваемый колесом:

H _т= 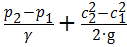(2.3)

Сучетом того, что каждый килограмм жидкости проходя через рабочее колесо, получает приращение энергии за счет центробежной силы, равной произведению массы частицы на ускорение, то баланс энергии для 1 кг жидкости будет иметь вид:

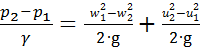. (2.4)

Подставляя в уравнение (2.3) выражение (2.4) получим:

H _т= + + .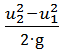

Первый член этого уравнения представляет приращение напора, вызываемого центробежными силами, действующими на массы жид­ кости, перемещающейся от r₁ до r₂; второй член показывает измене­ние кинетической (скоростной) энергии потока от входа до выходаиз рабочего колеса. Последний член представляет изменение напора

-44-

в результате изменения относительной скорости потока при проте­кании жидкости через рабочее колесо.

Пользуясь зависимостями (2.1) и (2.2) заменим ω ₁ и ₂ соответ­ственно через с_1, и₁ и с₂, и_г После сокращений получим:

H _т= 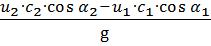(2.5)

Это и есть основное уравнение Эйлера для определения теорети­ческого напора колеса турбомашины, написанное в самом общем виде и справедливое для всех лопастных машин, т.е. водяных паровых и газовых турбин, центробежных насосов и вентиляторов, а также тур­бокомпрессоров. В результате гидравлических сопротивлений про­теканию жидкости через рабочее колесо, на преодоление которых зат­рачивается часть энергии, действительный напор, создаваемый насо­сом, меньше теоретического. Введя в уравнение (2.5.) гидравличес­кий коэффициент полезного действия учитывающий уменьшение теоретического напора, получим значение теоретического напора:

H _т= · 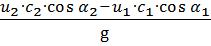(2.6)

В центробежном насосе во избежание лишних потерь важно со­блюдать условие безударного входа жидкости в рабочее колесо. Для этого жидкость подводят к насосу так, чтобы скорость с₀ жидкости перед входом в колесо была направлена в плоскости, проходящей че­рез ось насоса, и чтобы абсолютная скорость с₁ жидкости не изменя­лась или же по возможности мало отличалась по направлению и ве­личине от скорости с₀, т.е. с₁=с₀

В соответствии с этим α₁=90°, а второй член правой части равенства (2.6) превратится в ноль и уравнение Эйлера примет следующий вид:

H _т= 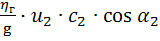(2.7)

Это и есть основное уравнение центробежного насоса.

Дата добавления: 2014-11-06