Комплексный чертеж плоскости

Натуральная величина отрезка прямой общего положения равна гипотенузе пря-моугольного треугольника, один катет которого равен проекции отрезка в какую-либо плоскость проекций, а другой - разности удалений концов отрезка от той же плоскости проекций, на которой взят первый катет треугольника. Чтобы определить угол наклона прямой к какой-либо плоскости проекций, при построении прямоугольного треугольника в качестве первого катета нужно взять проекцию отрезка в эту плоскость.

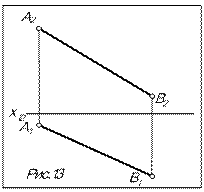Задача. Определить НВ отрезка АВ и угла наклона его к П₂ (рис.13)_.

Алгоритм решения

1.Т.к. АВ – отрезок общего положения, то для решения применяем метод прямоугольного треугольника.

2.Т.к. нужно определить угол наклона к П₂, то при по-строении прямоугольного треугольника в качестве первого катета берем фронтальную проекцию А₂В₂.

3.Из В₂ (можно из А₂) проводим перпендикуляр к А₂В₂ и в качестве второго катета откладываем разность глубин концов отрезка D f.

А₂В₀ – натуральная величина отрезка, b - угол на­клона его к П₂.

Задача. На прямой l отложить отрезок АВ = 40 мм (рис.14).

Алгоритм решения

1.Т.к. прямая l – общего положения, отложить от точки А отрезок, равный 40мм нельзя: на прямой общего положения отрезки проецируются с искажением.

2.Чтобы построить такой отрезок применяем метод пря-моугольного треугольника: берем на прямой l произ-вольную точку С и определяем НВ отрезка АС, взяв в качестве первого катета его горизонтальную проекцию, а в качестве второго - разность высот его концов. На построенной НВ отрезка АС откладываем от А₀ нужную длину.

3. Из построенной точки В₀ опускаем перпендикуляр на l₁ и находим горизонтальную проекцию точки В₁, а по принадлежности l и её фронтальную проекцию. Отрезок АВ имеет нужную длину.

3.1.2.Прямая уровня

Определение: прямая, параллельная какой-либо плоскости проекций.

Признак: проекция прямой уровня в непараллельную плоскость – парал-лельна оси проекций.

Свойства чертежа: в параллельную плоскость проекций отрезок прямой и углы наклона её к плоскостям проекций проецируются в натуральную величину (рис.15, 16).

3.1.3.Проецирующая прямая

Определение: прямая, перпендикулярная какой-либо плоскости проекций (рис.17).

Признак: проекция прямой в перпендикулярную плоскость – точка, в параллельные – прямые перпендикулярные соответствующим осям проекций (рис.17-18).

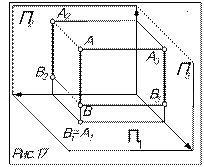Свойства чертежа: в параллельную плоскость проекций отрезок прямой проецируется в натуральную величину.

3.2.Взаимное положение прямых

Прямые в пространстве могут располагаться параллельно друг другу, пересекаться или скрещиваться.

Если прямые параллельны, то их одноименные проекции параллельны (или совпадают) (рис 19).

Если прямые пересекаются, то их одноименные проекции пересекаются (или совпадают), при этом точки пересечения проекций лежат на одной линии связи (рис.20).

Если прямые скрещиваются, то точки пересечения одноименных проекций не лежат на одной линии связи. Точки пересечения проекций- совпадающие проекции конкурирующих точек, принадлежащих скрещивающимся прямым (рис.21).

Плоскость считается заданной на чертеже, если:

-возможно построить проекции любой точки, принадлежащей плоскости;

-возможно определить, принадлежит ли данной плоскости заданная на чертеже точка.

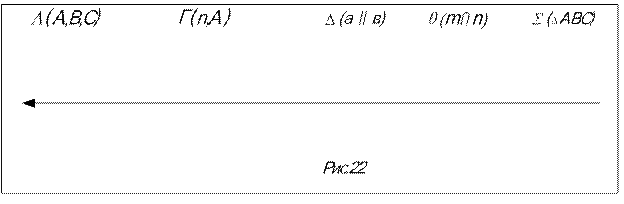
В общем случае плоскость задается на чертеже проекциями своего определителя, под которым понимается совокупность элементов, однозначно задающих плоскость в пространстве (рис.22): три точки, не лежащие на одной прямой, прямая и точка вне прямой, две пересекающие прямые, две параллельные прямые, плоская фигура.

4.1.Положение плоскости относительно плоскостей проекций

4.1.1.Плоскость общего положения

Определение: плоскость, наклоненная ко всем плоскостям проекций (рис.23).

Признак: ни на одну из плоскостей проекций определитель плоскости не проецируется на прямую (см. рис.22).

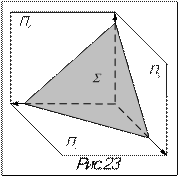Свойства чертежа: фигура в плоскости общего положения, углы наклона её к плоскостям проекций ни на одну плоскость проекций не проецируется в натуральную величину.

Восходящей называется плоскость, высота точек которой возрастает по мере удаления от наблюдателя, а нисходящей - плоскость, высота точек которой уменьшается по мере удаления от наблюдателя. Признак: у восходящей плоскости обход проекцийточек на обеих плоскостях проекций одинаковый (плоскости L и q на рис.22), у нисходящей – противоположный (плоскость S на рис.22). У восходящей плоскости видна на П₁ и П₂ одна и та же сторона, у нисходящей - разные стороны.

4.1.2. Проецирующая плоскость

Определение: плоскость, перпендикулярная какой-либо плоскости проекций (рис.24).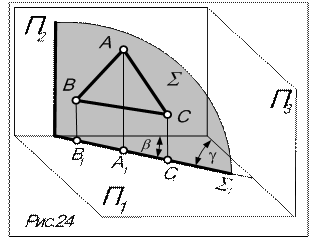

Признак: проекция плоскости на перпендикулярную плоскость проекций – прямая (вырожденная проекция плоскости), наклоненная к осям проекций (S на рис.24,25). На комплексном чертеже проецирующие плоскости задаются, как правило, своими вырожденными проекциями (см. рис.25).

Свойства чертежа:вырожденная проекция обладает собирательным свойством: проекция фигуры, расположенной в плоскости, в перпендикулярную плоскость проекций располагается на вырожденной проекции проецирующей плоскости. Углы наклона вырожденной проекции к осям проекций равны углам наклона плоскости к соответствующим плоскостям проекций.

В зависимости от плоскости проекций, к которой перпендикулярна плоскость, проецирующие плоскости называются горизонтально, фронтально или профильно проецирующими.

4.1.3.Плоскость уровня

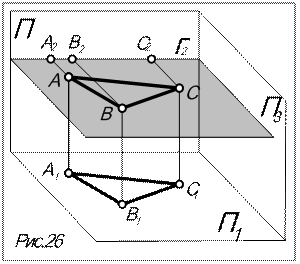Определение: плоскость, параллельная какой-либо плоскости проекций (рис.26).

Признак: проекция плоскости на перпендикулярную плоскость проекций – прямая (вырожденная проекция) Г₂, параллельная осям проекций (рис.27).

Свойства чертежа: фигура в плоскости уровня в параллельную плоскость проекций проецируется в натуральную величину.

4.2.Принадлежность прямой и точки плоскости

Прямая принадлежит плоскости:

а) если прямая проходит через две точки, принадлежащие плоскости;

б) если прямая проходит через точку плоскости и параллельна прямой, лежащей в плоскости.

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости.

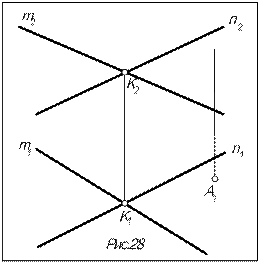
Задача. Построить недостающую проекцию точки А, принадлежащей плоскости S (m n) (рис.28).

Алгоритм решения

1. Через известную горизонтальную А₁ проекцию точки А проводим проекцию произвольной пря-мой l так, чтобы она пересекала прямые m и n, за-дающие плоскость S: А₁ Î l₁

2. Находим проекции точек 1 и 2 пересечения прямой l с прямыми m и n:

1₁ = l₁ m₁, 2₁ = l₁ n₁ , 1₂ Î m₂ , 2₂ Î n₂ .

3. Соединив 1₂ и 2₂ , получаем фронтальную l₂ проекцию прямой l, по принадлежности которой и находим фронтальную проекцию точки А: А₂ Î l ₂.

4.3.Прямые особого положении в плоскости

4.3.1.Прямая уровня плоскости

Определение: прямая, принадлежащая плоскости и параллельная какой-либо плоскости проекций.

Задача. В плоскости q (D АВС) провести произвольные горизонталь и фронталь (рис 29).

Алгоритм решения

1.Т.к. требуется построить произвольные горизонталь и фронталь, то для удобства построений проведем их соответственно через вершины С и А треугольника.

2. Сначала проводим те проекции прямых, направление которых известны – фронтальную проекцию горизонтали h₂ и горизонтальную фронтали f₁: C₂ Î h₂ X₁₂, А₁ Î f₁ X₁₂ .

3. Недостающие проекции прямых находим по принадлежности их плоскости треугольника АВС, а именно по двум точкам ей принадлежащим. Для этого находим точки 1 и 2 пересечения горизонтали и фронтали со сторонами АВ и ВС соответственно и соединяем их с одноименными проекциями А и С.

В проецирующей плоскости пря-мая уровня, параллельная неперпендику-лярной плоскости проекций – прое-цирующая прямая (рис.30).

4.3.2.Прямая наибольшего наклона плоскости к какой-либо плоскости проекций

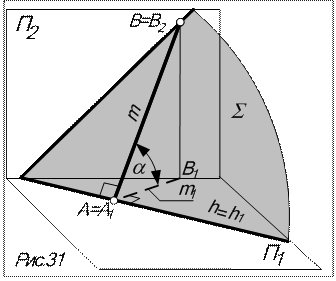Определение: прямая, лежащая в плоскости, и перпендикулярная соответствующей линии уровня плоскости.

Признак: в плоскость проекций, параллельную линии уровня, прямой угол между линией наибольшего на-клона и линией уровня проецируется в натуральную величину.

Прямая наибольшего наклона используется для определения вели-чины двугранного угла между плос-костью общего положения и какой-либо плоскостью проекций: двугран-ный угол измеряется линейным углом между линией наибольшего наклона плоскости и ее проекцией на соответствующую плоскость проекций.

На рис.31 показана прямая наибольшего наклона m плоскости å к горизонтальной плоскости проекций (линия ската), проведенная перпендикулярно горизонтали h. При этом m₁ ^ h ₁. Угол a между линией ската m и её проекцией m₁ и есть угол между плоскостями å и П_{1 .}

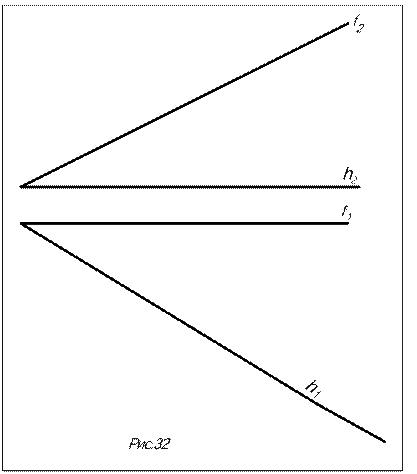
Задача. Определить углы наклона плоскости S (f h) к плоскостям проекций П₁ и П₂ (рис.32).

Алгоритм решения

1.Определение угланаклона å к П_{1 .}

1.1.Проводим произволь-ную линию ската m: сначала её горизонтальную проекцию m₁ ^ h₁, а затем, по двум то-чкам 1 и 2 пересечения линии ската с горизонталью и фрон-талью плоскости, её фронта-льную проекцию 1₂ m₂ 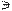2₂. 1.2. Строим прямоугольный треугольник для определения натуральной величины отрезка (12): в качестве первого катета берём горизонтальную проекцию отрезка (1₁2₁), а в качестве второго – разность высот Dh точек 1 и 2. Угол между натуральной величиной (2₁1₀) отрезка и его проекцией (1₁2₁) и есть искомый угол a наклона плоскости å к П₁

2. По аналогичному алгоритму, проведя линию n наибольшего наклона плоскости å к П₂, находим угол b.

Дата добавления: 2014-11-06