Способы преобразования чертежа

S (l n) ^ D (f h).

Цель преобразования – упростить чертеж, расположив заданные геометрические фигуры в более удобное для решения задачи частное положение.

Основными задачами преобразований являются:

1. Прямую общего положения сделать прямой уровня.
2. Прямую общего положения сделать проецирующей прямой.
3. Плоскость общего положения сделать проецирующей.
4. Плоскость общего положения сделать плоскостью уровня.

6.1.Замена плоскостей проекций

При этом способе преобразования чертежа положение фигуры в пространстве не изменяется, а заменяют одну из основных плоскостей проекций, проводя новую – до-полнительную – плоскость проекций так, как это удобно для решения задачи. При этом новая плоскость должна быть перпендикулярной незаменяемой плоскости проекций.

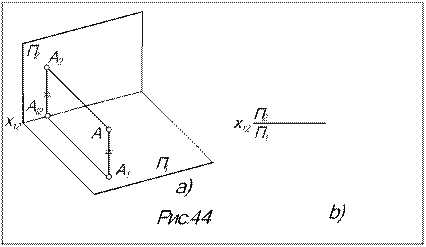Рассмотрим этот способ на простейшем примере, когда фигурой в пространстве является точка. Допустим, в системе плоскостей проекций П₁/П₂, где расположена точка А (рис.44а), решение задачи затруднено или вообще невозможно. Поэтому плоскость П₂ заменяется на дополнительную плоскость П₄, которую располагают так, чтобы решение было облегчено. В новой системе П₁ / П₄ c новой осью проекций s₁₄ необходимо построить проекцию точки А₄. По методу ортогонального проецирования из точки А опускается перпендикуляр на П₄, а для нахождения точки его пересечения с П₄ (проекции А₄) через А₁ проводится ломаная А₁А₁₄А₄, оба звена которой перпендикулярны оси системы s₁₄.

При переходе к новой системе плоскостей проекций остаются неизменными:

- одна из плоскостей проекций и проекция фигуры в ней (в нашем случае П₁ и А₁),

- расстояние от фигуры до незаменяемой плоскости проекций (АА₁), которое проецируется в натуральную величину как в замененную, так и новую плоскости проекций (АА₁=А₂А₁₂ = А₄А₁₄).

Для преобразования пространственной конструкции (рис.44а) в плоское изображение (чертеж) плоскость П₁ вращением вокруг оси x₁₂ совмещается с П₂, а новая плоскость П₄ вращается вокруг оси s₁₄ до совмещения с П₁. При этом ломаная А₁А₁₄А₄ превращается линию связи, перпендикулярную оси s₁₄ (рис.44б).

Построение проекции точки в дополнительную плоскость проекций формализуется следующим алгоритмом:

Дата добавления: 2014-11-06