Точка принадлежит поверхности, если она лежит на линии, этой поверхности принадлежащей

ПОВЕРХНОСТИ ВРАЩЕНИЯ

Поверхностью вращения называется поверхность, образованная при вращении линии (образующей) вокруг неподвижной оси. В инженерной практике поверхности вращения задаются, как правило, своими очерками (рис.73,74). На рис. 74 показаны наиболее часто встречающиеся в инженерной практике поверхности вращения.

10.1.Основные линии поверхности вращения.

Параллель - сечение поверхности вращения плоскостью, перпендикулярной оси вращения. Представляет собой окружность, которая на плоскость проекций, перпендикулярную оси, проецируется в натуральную величину, а в плоскость, параллельную оси, - в виде отрезка, перпендикулярного проекции оси и равного диаметру параллели. Наибольшая из близлежащих параллелей называется экватором, наименьшая - горлом.

Меридиан - сечение поверхности вращения плоскостью, проходящей через ось вращения.

Меридиан, расположенный в плоскости, параллельной плоскости проекций, называется главным меридианом и определяет очерк поверхности в этой плоскости.

С помощью этих линий «берутся» (строятся) точки, принадлежащие поверхности. При этом используется признак принадлежности точки поверхности:

Например, с помощью параллели радиуса R на по-верхности построены проекции точки А: через заданную фронтальную проекцию А₂ проведена проекция параллели, определен её радиус и построена её горизонтальная проекция, по принадлежности которой найдена горизонтальная проекция А₁. При этом заданному положению А₂ соответствуют два положения горизонтальной проекции точки: А₁, если точка А видима на П₂, и А₁^*, если она на П₂ невидима.

10.2.Пересечение криволинейной поверхности плоскостью

Поверхности вращения второго порядка пересекаются плоскостью по кривым второго порядка.

10.2.1.Cферические сечения. При пресечении сферы плоскостью всегда получается окружность.

10.2.2.Цилиндрические сечения. Вид цилиндрического сечения (рис.75) зависит от положения секущей плоскости относительно оси цилиндра:

1. Плоскость перпендикулярна оси i цилиндра – в сечении – окружность с центром О на оси i и радиусом, равным радиусу цилиндра

Г ^ i, Г Ф_цил = окружность n(О, R);

2. Плоскость параллельна оси цилиндра – в сечении две параллельных прямых – образующих цилиндра 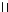D i, D Ф_цил = a и b;

3. Плоскость наклонена к оси i цилиндра – в сечении - эллипс m с центром О^* на оси i с большой осью АВ, величина которой зависит от угла наклона плоскости к оси, и малой осью CD, равной диаметру цилиндра

S i, S Ф_цил = эллипс m (О^*, AB, CD =R).

Цилиндрическая поверхность является проеци-рующей к плоскости проекций, перпендикулярной к оси цилиндра, поэтому в эту плоскость (на рис.75 в П₁) сечения цилиндра проецируются на окружность - вырожденную проекцию (очерк) поверхности.

10.2.3.Конические сечения. Вид сечения зависит от следующих факторов (рис.76):

1. Положение секущей плоскоcти относительно вершины конуса:

если плоскость проходит через вершину конуса (D S)- в сечении две пересекающиеся прямые (образующие конуса);

если плоскость не проходит через вершину - в сечении кривые второго порядка.

2. Угол a между секущей плоскостью и осью конуса:

если угол - 90°(Г ^ i), то в сечении окружность (О, r) (параллель конуса);

если угол не равен 90° - в сечении эллипс, парабола или гипербола.

3. Соотношение между углом b наклона секущей плоскости к оси конуса и углом a между осью конуса и его образующей:

а) b > a, S Ф_кон = эллипс; большая ось эллипса – АВ, малая – CD, центр эллипса О^* не лежит на оси конуса и находится делением АВ пополам (А₂О₂ = В₂О₂).

б) b = a, Q Ф_кон = парабола с вершиной F;

в) b < a, L Ф_кон = гипербола с вершинами в точках Р.

10.3.Построение сечения поверхности вращения плоскостью

Чтобы построить сечение, необходимо найти достаточное количество точек, ему принадлежащих, и прежде всего должны быть найдены особые точки сечения, к которым относятся:

· геометрически особые точки сечения (вершины, центры, точки на концах осей и т.п.)

· граничные точки видимости (опорные точки) – точки пересечения очерковых линий поверхности с секущей плоскостью.

Задача. Построить проекции и натуральную величину сечения конуса плоскостью S (рис.77) Алгоритм решения

1. Определяем вид сечения и его проекций. Т.к. S не проходит через вершину конуса S и угол b наклона её к оси конуса больше угла a между осью и образующей, то в сечении – эллипс + отрезок - результат пересечения секущей плоскости с плоскостью основания. Т.к. секущая плоскость - фронтально проецирующая, то на П₂ сечение проецируется в виде отрезка, лежащего на вырожденной проекции S₂ секущей плоскости внутри очерка конуса.

2. Находим особые точки сечения: центр эллипса, точки на концах его осей, граничные точки видимости. Чтобы построить эти точки необходимо обозначить очерковые образующие конуса: A₂S₂ , B₂S₂ на П₂ , C₃S₃ , D₃S₃ на П₃ и найти их проекции на остальных плоскостях. Сначала находим проекции особых точек сечения на его известной фронтальной проекции.

Продлив вырожденную проекцию S₂ секущей плоскости до пересечения с продолжением очерковой A₂S₂ , находим точку 2₂ – фронтальную проекцию точки, лежащей на конце большой оси (12) эллипса. Разделив пополам проекцию оси (1₂2₂), находим проекцию О₂ центра эллипса. Малая ось (34) эллипса является фронтально проецирующей и на П₂ спроецируется в точку – О₂ =3₂ =4₂.

Граничные точки видимости 5,6,7,8 находим на П₂ как результат пересечения вырожденной проекции плоскости с проекциями очерковых линий: 5₂ = С₂S₂ S₂, 6₂ = D₂S₂ S₂, 7₂ и 8₂ = m₂ S₂.

Найденные на П₂ точки строим на остальных плоскостях проекций. Точки на очерковых линиях находим по принадлежности этим линиям, проводя соответствующие линии связи, при этом для достижения требуемой точности построений не рекомендуется пользоваться постоянной чертежа к₀ и ломаными линиями связи между П₁ и П₃. Проведя горизонтальную линию связи через 5₂ = 6₂ и построив 5₃ Î C₃S₃ и 6₃ Î D₃S₃, замеряем расстояние между 5₃ , 6₃ и фронтальной плоскостью симметрии Ф (Ф₃). Отложив это расстояние по соответствующей вертикальной линии связи по обе стороны от Ф₁, находим горизонтальные проекции точек 5 и 6. По аналогичному алгоритму находим недостающие проекции точек 7 и 8: сначала на П₁, а затем и на П₃.

Недостающие проекции точек 3 и 4 находим по принадлежности конусу: через 3₂= 4₂ проводим фронтальную проекцию параллели радиуса r, строим эту параллель на остальных проекциях и по принадлежности ей находим горизонтальные, а затем и профильные проекции точек 3 и 4. По аналогичному алгоритму можно построить случайные точки сечения.

3. Соединяем одноименные проекции построенных точек с учетом видимости. Видимость определяем по представлению. На П₁ невидимым является отрезок (78), лежащий в основании конуса, невидимом при взгляде сверху, а на П₃ - участок эллипса (516), лежащий на правой половине боковой поверхности конуса, невидимой при взгляде слева.

4. НВ сечения находим заменой плоскостей проекций: П₁ 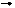П₄ 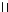å, П₁ / П₂ (x₁₂) 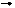П₂ / П₄ (s₂₄ 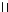S₂). Для удобства построений ось x₁₂ совмещаем проекцией плоскости симметрии Ф₁. Точки НВ находим по алгоритму построения проекций точек в дополнительную плоскость (см. стр.21, рис.44).

Если секущая плоскость - общего положения, то для упрощения решения заменой плоскостей проекций секущая плоскость преобразуется в проецирующую.

10.4.Пересечение поверхности прямой линией

В общем случае для построения точек пересечения прямой с поверхностью применяется метод вспомогательных секущих плоскостей по следующему алгоритму (рис.78):

1. Прямая l заключается в плоскость S, пересекающую поверхность Ф по геометрически простой линии: l Ì S Ф.

2. Строится линия m пересечения поверхности Ф вспомогательной плоскостью S:

m =S Ф.

3. Искомые точки 1 и 2 находим как результат пересечения заданной прямой l с построенной линией пересечения m: 1,2 = l m.

Задача. Построить точки пересечения прямой l с поверхностью сферы Ф (О^*,R) (рис. 79).

Алгоритм решения

1. Заключаем прямую l в горизонтально проецирующую плоскость S:l₁= S_1.

2. Строим линию пересечения плоскости S со сферой – окружность (О, r). На П₁ окружность проецируется в виде отрезка, расположенного внутри очерка сферы на вырожденной проекции S₁. Разделив отрезок пополам, находим проекцию центра О₁ и радиус r сечения. На П₂ окружность проецируется в виде эллипса, т.к. S на-клонена к П₂ . Построение эллипса - графически довольно сложная задача. Поэтому для упрощения решения вводим дополнительную плоскость П₄, расположив её параллельно S, и переходим к новой системе плоскостей проекций

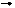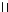П₁ / П₄ : П₂ П₄ S,

П₁ / П₂ (x₁₂) 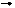П₁ / П₄ (s₁₄ 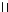S₁).

Строим в П₄ проекцию окружности, находя проекцию её центра по алгоритму построения точки в дополнительную плоскость.

Взяв на прямой l произвольные точки 1 и 2, строим их проекции на П₄ , соединив которые получаем проекцию прямой l₄

3. Находим точки А и В пересечения прямой l со сферой, сначала на П₄ как результат пересечения l₄ с проекцией окружности (О₄, r), а затем по принадлежности прямой l на остальных плоскостях проекций.

4. Видимость точек А и В и прямой l определяем по представлению, рассматривая проекции совместно с направлением взгляда на соответствующую плоскость проекций, как это показано на рис.79.

Дата добавления: 2014-11-06