Ортогональные проекции прямой и плоскости

Лекция 2

Линия - это множество всех последовательных положений движущейся точки. Прямая линия получается при движении точки без изменения направления. Две точки однозначно определяют положение прямой в пространстве.

Прямые в пространстве могут занимать:

1. общее положение;

2. частное положение.

Прямая, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется прямой общего положения. Она наклонена к плоскостям проекций под разными углами. Прямая линия бесконечна и пронизывает все плоскости проекций.

Образование комплексного чертежа прямой аналогично образованию комплексного чертежа точки. Для изображения прямой на чертеже необходимо иметь проекции определяющих ее точек.

Прямая общего положения и углы наклона прямой. Определение натуральной величины отрезка прямой общего положения.

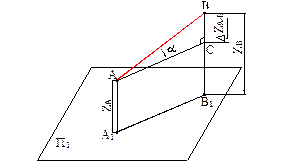
АВ – прямая общего положения; А₁В₁; А₂В₂– проекции прямой;

ZА, ZВ – координаты z точек А и В;

DZ = ZВ – ZА – разница координат точек А и В (по высоте).

a - угол наклона прямой к горизонтальной плоскости проекций, b - угол наклона прямой к фронтальной плоскости проекций g - угол наклона прямой к профильной плоскости проекций, D АСВ – прямоугольный треугольник.

Величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника. Один катет этого треугольника равен проекции отрезка, а второй – разности расстояний концов этого отрезка до плоскости, на которой строится прямоугольный треугольник.

Угол, заключенный между натуральной величиной отрезка и ее проекцией на данную плоскость, есть угол наклона прямой к этой плоскости.

Прямые частного положения

1. Прямые, çç одной из плоскостей проекций, называются прямыми уровня.

а) A₂B₂çç х; A₁B₁= çАВç- горизонтальная прямая уровня.

б) C₁D₁ççx; C₂D₂ = çCDç- фронтальная прямая уровня.

в) E₂F₂ ^ x; E₁F₁^ x; E₃F₃= çEFç - профильная прямая уровня.

2. Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими прямыми.

a) A’= B’; A”B” = çABç - горизонтально - проецирующая прямая.

б) С’D’ = çCDç; C” = D” – фронтально – проецирующая прямая.

в) E’F’ =çЕFç; E”F” = çEFç; E”’ = F”’ – профильно - проецирующая прямая.

Взаимное положение прямых в пространстве

1. Если прямые параллельны в пространстве, то их одноименные проекции параллельны.

2. Если прямые пересекаются в точке 1, то их одноименные проекции тоже пересекаются; при этом проекции точки пересечения обязательно располагаются на одной линии проекционной связи, перпендикулярной к оси.

3. Если прямые в пространстве скрещиваются, то их проекции могут пересекаться, но точки пересечения проекций не лежат на одной линии проекционной связи.

Плоскость. Способы задания плоскости. Положение плоскости в пространстве.

Плоскость образуется при движении одной прямой (образующей) по другой (направляющей).

Плоскость можно задать:

1. Тремя точками, не лежащими на одной прямой Q (A,B,C).
2. Прямой и точкой, не лежащей на этой прямой Q (A, BC).
3. Двумя параллельными прямыми Q (n || BC).
4. Двумя пересекающимися прямыми Q (n ∩ BC).
5. Плоской фигурой Q (ΔABC).
6. Следами Q (Qп₁, Qп₂).

Следом плоскости называется линия пересечения заданной плоскости с плоскостью проекций.

Способы задания плоскости

Положение плоскости в пространстве

1. Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций. Характерной особенностью плоскости общего положения на чертеже является то, что все проекции данной плоскости представляют собой плоскость, а не прямую, и ни на одну плоскость проекций плоскость не проецируется в натуральную величину.

Дата добавления: 2014-11-06