Принадлежность точки и прямой плоскости. Взаимное положение прямой и плоскости

Лекция 3

Фронтальная плоскость уровня

Плоскости частного положения

2.1. Проецирующие плоскости – плоскости перпендикулярные к одной из плоскостей проекций.

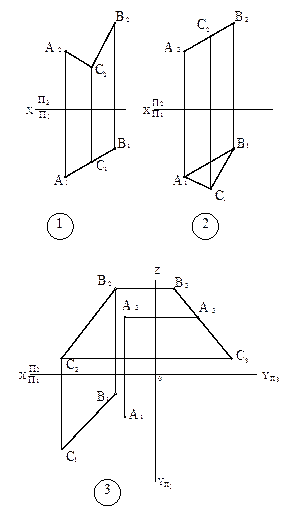
1. Горизонтально-проецирующая плоскость Q (АС∩ВС)_┴П₁.

2. Фронтально-проецирующая

плоскость Р (ΔАВС)_┴П₂.

3. Профильно-проецирующая

плоскостьS (А, ВС)_┴П₃.

2.3. Плоскости уровня – это плоскости, параллельные только одной из плоскостей проекций.

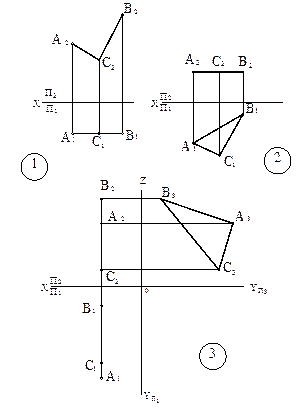
Q (АС∩ВС) || П₂.

2. Горизонтальная плоскость уровня Р (ΔАВС) || П₁.

3. Профильная плоскость уровня

S (А, ВС) || П₃.

Характерной особенностью плоскости уровня на чертеже является то, что плоскость проецируется на плоскость проекций, которой она параллельна, в натуральную величину.

1. Прямая принадлежит плоскости, если она проходит через две точки плоскости.
2. Прямая принадлежит плоскости, если она проходит через одну точку плоскости и параллельна прямой, принадлежащей плоскости.

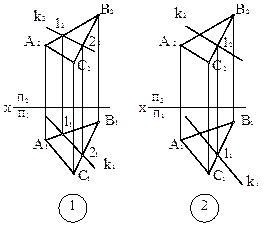
3. {(1 є АВ, 2 є ВС), (1є k, 2 є k),

следовательно, k є P (ΔABC)}.

4. {(1 є ВС, 1є k, k || AС),

следовательно, k є P (ΔABC)}.

1. Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей плоскости.

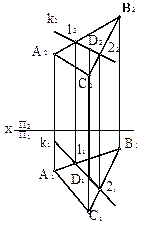
{(k є Δ AВС, D є k), следовательно, D є P (ΔABC)}.

Главные линии плоскости

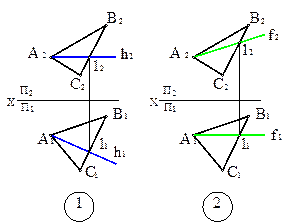
1. Горизонталь – это прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций.
2. Фронталь – это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций.

Проецирование прямого угла

Если две прямые пересекаются под прямым углом, то их проекции в общем случае образуют угол, не равный 90°. Для того, чтобы прямой угол проецировался в истинную величину, необходимо и достаточно, чтобы одна сторона прямого угла была параллельна плоскости проекций, а другая – не перпендикулярна плоскости проекций.

В₁1_{1 ┴} h₁,

С₂1_{2 ┴} f₂

Взаимное положение прямой и плоскости

Прямая и плоскость в пространстве может занимать следующие взаимные положения:

1. Прямая принадлежит плоскости (см. выше);
2. Прямая параллельна плоскости;
3. Прямая пересекает плоскость.
4. Прямая перпендикулярна плоскости.

Прямая параллельна плоскости

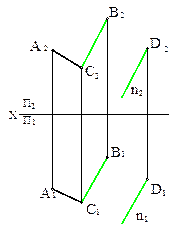
Прямая параллельна плоскости, если она параллельна хотя бы одной прямой, принадлежащей этой плоскости.

n2 ||B2C2; n1 ||B1C1;

ВС є P (BC ∩ AC)

следовательно, N || P (BC ∩ AC

Прямая пересекает плоскость

Если прямая и плоскость имеют одну общую точку, то прямая пересекает плоскость.

Рассмотрим четыре случая пересечения прямой и плоскости:

1. Прямая и плоскость находятся в проецирующем положении;

2. Плоскость находится в проецирующем положении, а прямая – в общем положении;

1. Прямая находится в проецирующем положении, а плоскость – в общем положении.
2. Прямая и плоскость находятся в общем положении.

Если прямая и плоскость занимают проецирующее положение, то построений точки пересечения не выполняют, а отмечают проекции искомой точки пересечения на чертеже:

- на одной плоскости проекций проекция точки пересечения прямой и плоскости находится в месте пересечения проекций прямой и плоскости;

- на другой плоскости проекций проекция точки пересечения прямой с плоскостью совпадает с проекцией прямой l.

Например (1):

- на фронтальной плоскости проекций проекция точки пересечения прямой и плоскости К (К₂) находится в месте пересечения проекций прямой l и плоскости ΔАВС;

- на горизонтальной плоскости проекций проекция точки пересечения прямой l с плоскостью ΔАВС - К (К₁) - совпадает с горизонтальной проекцией прямой l.

Видимость прямой l не определяется.

Если плоскость находится в проецирующем положении, а прямая – в общем положении, то построений точки пересечения выполняют в последовательности: отмечают одну проекцию искомой точки пересечения на чертеже, она находится в месте пересечения проекций прямой и плоскости, а вторую проекцию точки пересечения достраивают по линии проекционной связи.

Например (2):

- на фронтальной плоскости проекций проекция точки пересечения прямой и плоскости К (К₂) находится в месте пересечения проекций прямой l и плоскости ΔАВС;

- на горизонтальной плоскости проекций проекция точки пересечения прямой l с плоскостью ΔАВС - К (К₁) – достраивается по линиям связи на горизонтальной проекции прямой l.

Видимость прямой l определяется при помощи горизонтально-конкурирующих точек 1 и 2.

Если прямая находится в проецирующем положении, а плоскость – в общем положении, то

- на одной плоскости проекций проекция точки пересечения прямой с плоскостью совпадает с проекцией прямой;

- на другой плоскости проекций проекция точки пересечения прямой и плоскости достраивается при помощи вспомогательной прямой, принадлежащей заданной плоскости и проходящей через известную проекцию точки пересечения.

Например (3):

- К₁ - горизонтальная проекция точки пересечения прямой l с плоскостью ΔАВС совпадает с горизонтальной проекцией прямой l.

- К₂ – фронтальная проекция точки пересечения прямой и плоскости достраивается при помощи прямой 1-2, принадлежащей плоскости и проходящей через известную проекцию К₁.

Если прямая и плоскость находятся в общем положении, то для нахождения точки пересечения прямой и плоскости необходимо:

- через заданную прямую задать вспомогательную плоскость проецирующего положения;

- найти линию пересечения вспомогательной плоскости и заданной плоскости;

- найти точку пересечения линии пересечения и заданной прямой, которая будет являться точкой пересечения прямой и плоскости;

- определить видимость прямой относительно заданной плоскости на плоскостях проекций при помощи одной пары конкурирующих точек на каждой из плоскостей проекций.

Например (4):

- заключить прямую l во вспомогательную секущую плоскость Q фронтально-проецирующего положения и определить линию пересечения плоскости Q и заданной плоскости ΔАВС (сначала 1₂- 2₂ , затем 1₁- 2₁ );

- найти точку пересечения прямой l и линии пересечения – К (сначала К₁, затем К₂);

- видимость прямой l на фронтальной плоскости проекций определяется фронтально-конкурирующей парой 2=3, а на горизонтальной плоскости – горизонтально-конкурирующей парой 4=5.

Прямая перпендикулярна плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим данной плоскости. Следовательно, фронтальная проекция этой прямой должна быть перпендикулярна фронтальной проекции фронтали заданной плоскости, а горизонтальная проекция прямой должна быть перпендикулярна горизонтальной проекции горизонтали.

Р_{1 ┴} А₁1₁

Р_{2 ┴} А₂2₂, следовательно, Р _┴ Q (ΔАВС)

Взаимное положение плоскостей

Плоскости могут быть параллельными, перпендикулярными и пересекаться.

1. Если две пересекающиеся прямые одной плоскости взаимно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости взаимно параллельны.

АС ∩ ВС є Р

DF ∩ FE є Q

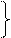
АС || DF

BC || FE, следовательно,

плоскость Р || плоскости Q

1. Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

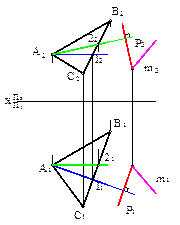
Плоскость Р (ΔАВС) _┴ плоскости Q (p ∩ m),

т.к. прямая р _┴ ΔАВС.

1. Взаимно-пересекающиеся плоскости.

3.1. Построение линии пересечения двух плоскостей, находящихся в проецирующем положении.

Плоскость Р (k || l) _┴ П₂, плоскость Q (m || n) _┴ П₂,

Р (k || l) ∩ Q (m || n) ═ f (f₁, f₂)

Видимость плоскостей на горизонтальной плоскости проекций определяется направлением взгляда: обе плоскости невидимые по обе стороны от линии пересечения.

3.2.Построение линии пересечения двух плоскостей, одна из которых находится в общем положении, а другая – в проецирующем.

Плоскость Р (k || l) _┴ П₂, плоскость Q (Δ АВС) - общего положения,

Р (k || l) ∩ Q (m || n) ═ 1-2 (1₁- 2₁, 1₂-2₂)

Линия пересечения плоскостей на фронтальной плоскости

проекций частично совпадает с фронтальной проекцией плоскости Р (k || l) – проекция отрезка 1-1 (1₂-2₂).

Линия пересечения на горизонтальной плоскости проекций достраивается по точкам, принадлежащим плоскости треугольника АВС – 1₁-2₁.

Видимость плоскостей на горизонтальной плоскости проекций определяется направлением взгляда на горизонтальную плоскость.

Дата добавления: 2014-11-06